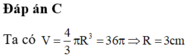Các câu hỏi tương tự
Gọi (S ) là khối cầu bán kính R, (N) là khối nón có bán kính đáy R và chiều cao h. Biết rằng thể tích của khối cầu (S) và khối nón (N) bằng nhau, tính tỉ số
h
R
. C. 12 D. 4
Đọc tiếp
Gọi (S ) là khối cầu bán kính R, (N) là khối nón có bán kính đáy R và chiều cao h. Biết rằng thể tích của khối cầu (S) và khối nón (N) bằng nhau, tính tỉ số h R .
![]()
![]()
C. 12
D. 4
Tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó là
Đọc tiếp
Tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó là

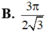
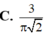
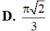
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh 3a, cạnh bên SC2a và SC vuông góc với mặt phẳng đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh 3a, cạnh bên SC=2a và SC vuông góc với mặt phẳng đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp S.ABC
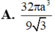
![]()
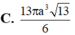
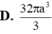
Cho khối chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh bằng 1, SA1 và SA
⊥
(ABC) . Tính thể tích của khối chóp đã cho.
Đọc tiếp
Cho khối chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh bằng 1, SA=1 và SA ⊥ (ABC) . Tính thể tích của khối chóp đã cho.
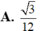
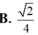
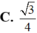
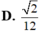
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE2EC. Tính thể tích V của khối tứ diện SEBD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE=2EC. Tính thể tích V của khối tứ diện SEBD.
![]()
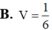
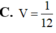
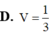
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc BAD
60
o
AB’ hợp với đáy (ABCD) một góc
30
o
Thể tích khối hộp là:
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc BAD= 60 o AB’ hợp với đáy (ABCD) một góc 30 o Thể tích khối hộp là:
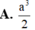
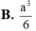
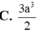
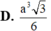
Một khối nón có diện tích đáy bằng 9p và diện tích xung quanh bằng 15p. Tính thể tích V của khối nón.
Đọc tiếp
Một khối nón có diện tích đáy bằng 9p và diện tích xung quanh bằng 15p. Tính thể tích V của khối nón.
![]()
![]()
![]()
![]()
Cho lăng trụ đứng ABCD.ABCD có đáy là hı̀nh thoi cạnh 3a, góc
B
A
D
^
120
0
. Tı́nh thể tı́ch khối lăng trụ đã cho
A
.
2
3
a
3
B
.
27
3...
Đọc tiếp
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là hı̀nh thoi cạnh 3a, góc B A D ^ = 120 0 . Tı́nh thể tı́ch khối lăng trụ đã cho
A . 2 3 a 3
B . 27 3 a 3 2
C . 40 3 a 3
D . 3 a 3
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Tính thể tích nước còn lại trong bình.
Đọc tiếp
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Tính thể tích nước còn lại trong bình.
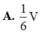
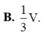
![]()
![]()