Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC; CA: AB.Tìm mệnh đề đúng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
cho tam giác ABC, đường trung tuyến BD. Trên tia đối của BD lấy E sao cho DE=DB. Gọi M, N lần lượt là trung điểm của BC và EC. Gọi P, Q lần lượt là giao điểm của AM, AN với BE. CMR BP=PQ=QE2cho tam giác ABC, đường trung tuyến BD. Trên tia đối của BD lấy E sao cho DE=DB. Gọi M, N lần lượt là trung điểm của BC và EC. Gọi P, Q lần lượt là giao điểm của AM, AN với BE. CMR BP=PQ=QE
cho tam giác ABC(AB<AC<BC).Gọi M,N lần lượt là trung điểm của BC,AC.Đường thẳng vuông góc với M và N cắt nhau tại O. Gọi H,G lần lượt là trực tâm và giao điểm của các đường trung tuyến tam giác ABC.
CMR:GH=2GO,
Bài 5: Cho tam giác ABC vuông tại A,
AB=12 cm BC=13 cm .
Gọi M, N lần lượt là trung
điểm của AB và BC
a) Chứng minh
MN vuông góc AB
b) Tính độ dài MN
Bài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi I
là giao điểm của AP và MN. C/m: a) IA = IP b) IM = IN.
Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểm
của DH, M là trung điểm của HC.
C/m:a) IM vuông góc AD b) AI vuông góc DM.
. Cho tam giác ABC. Gọi M và N lần lượt là trung điểm của AB và AC. Lấy điểm D và E sao cho N là trung điểm của BD và M là trung điểm của CE. CMR: a) Tam giác AND = tam giác CNB b) AD=BC ; AD//BC c) A là trung điểm của ED.
a) Xét tam giác AND và tam giác CNB ta có:
NB = ND (Vì N là trung điểm của BD)
góc AND = góc CNB (đối đỉnh)
NA = NC (Vì N là trung điểm của AC)
=> tam giác AND = tam giác CNB (c-g-c)
b) Vì tam giác AND = tam giác CNB
=> AD = BC (2 cạnh tương ứng)
=> góc DAN = góc BCN (2 góc tương ứng)
mà góc DAN và góc BCN là 2 góc so le trong
suy ra AD // BC
c) chưa nghĩ ra
Cho tam giác ABC gọi M và N lần lượt là trung điểm của AB và AC.Vẽ điểm D và E sao cho N là trung điểm của BD và M là trung điểm của CE.CMR:
a) Tam giác AND= Tam giác CNB
b)AD=BC,AD song song BC
Cho tam giác ABC có BC = 16 cm. Gọi D và E lần lượt là trung điểm của AB và AC. Gọi M và N lần lượt là trung điểm của BD và EC. Tính MN?
A. 9cm
B. 8cm
C. 10cm
D. 12cm
* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
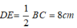
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB, AC. Vẽ D, E sao cho N là trung điểm của BD, M là trung điểm của CE. CMR:
a) tam giác AND = tam giác CNB
b) AD = BC, AD // BC
c) A là trung điểm của ED
Cho tam giác ABC = tam giác DEF . Gọi M và N lần lượt là trung điểm của BC , EF . Chứng minh AN=BN
Bài 2: Cho tam giác ABC. Gọi M và N lần lượt là trung điểm của AB và AC. Vẽ điểm D và E sao cho N là trung điểm của BD và M là trung điểm của CE. Chứng minh rằng;
a) tam giác AND = tam giác CNB
b) AD = BC; AD // BC. c) A là trung điểm của ED.
(VẼ HÌNH LUÔN NHA!)
a) Xét ΔAND và ΔCNB có
NA=NC(N là trung điểm của AC)
\(\widehat{AND}=\widehat{CNB}\)(hai góc đối đỉnh)
ND=NB(N là trung điểm của BD)
Do đó: ΔAND=ΔCNB(c-g-c)
b) Ta có: ΔAND=ΔCNB(cmt)
nên AD=BC(hai cạnh tương ứng)
Ta có: ΔAND=ΔCNB(cmt)
nên \(\widehat{ADN}=\widehat{CBN}\)(hai góc tương ứng)
mà \(\widehat{ADN}\) và \(\widehat{CBN}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Cho tam giác ABC. Gọi M,N,K lần lượt là trung điểm của AB,AC,BC.
Tính chu vi tam giác MNK cho biết tam giác ABC=24cm