Cho tập S = {1;2;3;...;19;20} gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc S. Xác suất để ba số lấy được lập thành một cấp số cộng là
A . 7 38
B . 5 38
C . 3 38
D . 1 114
Cho tập hợp S = (m - 1; m + 1)\(-∞; 1]. Giá trị của m để S chỉ có 1 tập con là:
A. m ≤ 0
B. m < 1
C. m > 1
D. m ≥ 0
Đáp án: A
S chỉ có 1 tập con
⇔ S = ∅ ⇔ (m - 1; m + 1) ⊂ (-∞; 1].
⇔ m + 1 ≤ 1 ⇔ m ≤ 0
cho mình xin đề toán bài 50,51,52 sách bài tập trang 17 lớp 7 tập 1
và bài 57,58,59 sách bài tập trang 18 lớp 7 tập 1
Bạn gõ tên mấy bài tập đó ra rồi tìm trên hoc24 cx có đó bạn
Cho S là tập hợp tất cả caccs giá trị nguyên của tham ssos m sao cho bất phương trình \(\dfrac{(m+1)x^2+\left(4m+2\right)x+4m+4}{mx^2+2\left(2m+1\right)x+m}\le1\) có tập nghiệm là R . Tính số phần tử của tập hợp S
Cho hàm số f ( x ) = ax 3 + bx 2 + cx + d có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của m(m∈R) sao cho (x-1) [ m 3 f ( 2 x - 1 ) - mf ( x ) + f ( x ) - 1 ] ≥0 ∀x∈R. Số phần tử của tập S là
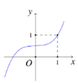
A. 2
B. 0
C. 3
D. 1
Cho hệ phương trình 2 x − y − 2 y + x = 2 y 2 x + 1 = m + 2 2 .2 y . 1 − y 2 ( 1 ) , m là tham số. Gọi S là tập các giá trị nguyên để hệ (1) có một nghiệm duy nhất. Tập S có bao nhiêu phần tử?
A. 0
B. 1
C. 3
D. 2
Chọn B.
Phương pháp:
+ Biến đổi phương trình thứ nhất của hệ để đưa về dạng
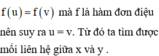
+ Thay vào phương trình thứ hai ta được phương trình ẩn y. Lập luận phương trình này có nghiệm duy nhất
thì hệ ban đầu sẽ có nghiệm duy nhất.

+ Sử dụng bất đẳng thức Cô-si để thử lại m.
Cách giải:



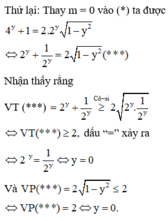
Vậy phương trình (***) có nghiệm duy nhất y = 0.
Kết luận : Với m = 0 thì hệ đã cho có nghiệm duy nhất nên tập S có một phần tử.
Chú ý :
Các em có thể làm bước thử lại như sau :
Thay m = 0 vào (*) ta được
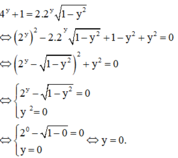
A là tập hợp các h/s giỏi môn Văn của 1 lớp, B là tập hợp cac h/s giỏi môn Toán của lớp đó;
a) A là tập hợp các số chia hêt cho 5, B là tập hợp các số chia hết cho 10
b) A là tập hợp các số chẵn, B là tập hợp các số lẻ
tìm x thuộc z (tập hợp z) sao cho (x+8)chia hết(x-1)
x + 8 chia hết cho x - 1
=> x - 1 + 9 chia hết cho x - 1
Có x - 1 chia hết cho x - 1
Vì x thuộc Z => x - 1 thuộc Z
=> 9 chia hết cho x - 1
=> x - 1 thuộc Ư(9)
=> x - 1 thuộc {1; -1; 3; -3; 9; -9}
=> x thuộc {2; 0; 4; -2; 10; -8}
Cho số hữu tỉ x = \(\frac{a-20}{-3}\), gọi S là tập hợp tất cả các số nguyên dương của a để x là 1 số hữu tỉ dương.
a) Viết tập hợp S theo 2 cách
b) Tính số tập hợp con có 2 phần tử từ tập S.
Để \(x=\frac{a-20}{-3}\) ( a ∈ N* ) nhận giá trị dương
=> a - 20 nhận giá trị âm
=> a nhỏ hơn 20
a) S = { a ∈ N* | a < 20 }
\(S=\left\{...;17;18;19\right\}\)
b) ( Không hiểu đề , thông cảm , bạn làm nốt nhé ! )
uuuuuuuuuuuuuuuuuuuuuuuuuuuuu
Câu b)
Số tập hợp con có 2 phần tử từ tập S là
\(C^2_{17}=171\)(tập hợp con)
VẬY....
Cho phương trình 2 - m 3 - 3 m 2 + 1 . log 81 x 3 - 3 x 2 + 1 + 2 + 2 - x 3 - 3 x 2 + 1 - 2 . log 3 1 m 3 - 3 m 2 + 1 + 2 = 0 . Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có số nghiệm thuộc đoạn 6 ; 8 . Tính tổng bình phương tất cả các phần tử của tập S.
A. 20
B. 28
C. 14
D. 10