Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x − 1 x − m nghịch biến trên khoảng − ∞ ; 2 .
A. 1 , + ∞
B. 2 , + ∞
C. 2 , + ∞
D. 1 , + ∞
Đáp án là C
Tập xác định : D = R \{m}
Ta có : y ' = 1 − m x − m 2
Hàm số nghịch biến trên khoảng (−¥;2) khi và chỉ khi y' <0, "x < 2, tức là : 1 − m < 0 m ≥ 2 ⇔ m ≥ 2 . Vậy tập giá trị m cần tìm là [2; + ∞ )
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 4 - 2 ( m - 1 ) x 2 + m - 2 đồng biến trên khoảng (1;3).
A. 
.
B. 
.
C. 
.
D. 
.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 4 - 2 ( m - 1 ) x 2 + m - 2 đồng biến trên khoảng (1;3)?
A. m ∈ [ - 5 ; 2 )
B. m ∈ (- ∞ ;2]
C. m ∈ ( 2 ; + ∞ )
D. m ∈ ( - ∞ ; - 5 )
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m 3 x 3 + 7 m x 2 + 14 x - m + 2 nghịch biến trên nửa khoảng [ 1 ; + ∞ ) ?
A. - ∞ ; - 14 15
B. ( - ∞ ; - 14 15 ]
C. - 2 ; - 14 15
D. [ - 14 15 ; + ∞ )
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 4 - 2 n - 1 x 2 + m - 2 đồng biến trên khoảng (1; 3)?
A. m ∈ [ - 5 ; 2 )
B. m ∈ ( - ∞ ; 2 ]
C. m ∈ 2 ; + ∞
D. m ∈ - ∞ ; - 5
Chọn B.
Tập xác định D = R.
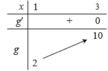
Dựa vào bảng biến thiên, kết luận: m ≤ min g(x) ⇔ m ≤ 2
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = f x = m x 3 3 + 7 m x 2 + 14 x - m + 2 giảm trên nửa khoảng [ 1 ; + ∞ ) ?
A. - ∞ ; - 14 15
B. ( - ∞ ; - 14 15 ]
C. - 2 ; - 14 15
D. [ - 14 15 ; + ∞ )
Chọn B.
Tập xác định D = R, yêu cầu của bài toán đưa đến giải bất phương trình
Tương đương với
Dễ dàng có được g(x) là hàm tăng 
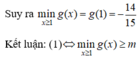
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 4 x + m giảm trên khoảng ( - ∞ ; 1 ) ?
A. -2<m<2
B. - 2 ≤ m ≤ - 1
C. - 2 < m ≤ - 1
D. - 2 ≤ m ≤ 2
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 4 x + m giảm trên khoảng - ∞ ; 1
A. - 2 ≤ m ≤ 2
B. - 2 < m < 2
C. - 2 ≤ m ≤ - 1
D. - 2 < m ≤ - 1
Chọn đáp án D
.
Ta có y ' = m 2 - 4 x + m 2 .
Hàm số luôn đơn điệu trên từng khoảng - ∞ ; - m và - m ; + ∞ .
Hàm số giảm trên khoảng - ∞ ; 1 tức là hàm số nghịch biến trên khoảng - ∞ ; 1 .
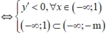
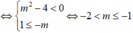
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 4 x + m giảm trên khoảng (-∞;1)?
A. -2≤ m ≤ 2
B. -2< m < 2
C. -2≤ m ≤ -1
D. -2< m ≤ -1
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = f ( x ) = m x 3 3 + 7 m x 2 + 14 x - m + 2 giảm trên nửa khoảng [ 1 ; + ∞ ) ?
A. - ∞ ; - 14 15
B. ( - ∞ ; - 14 15 ]
C. - 2 ; - 14 15
D. [ - 14 15 ; + ∞ )
.
với 
, 
, 
.
.
