Chọn B.
Tập xác định D = R, yêu cầu của bài toán đưa đến giải bất phương trình
![]()
Tương đương với
![]()
Dễ dàng có được g(x) là hàm tăng ![]()
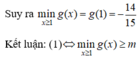
![]()
Chọn B.
Tập xác định D = R, yêu cầu của bài toán đưa đến giải bất phương trình
![]()
Tương đương với
![]()
Dễ dàng có được g(x) là hàm tăng ![]()
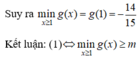
![]()
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = f ( x ) = m x 3 3 + 7 m x 2 + 14 x - m + 2 giảm trên nửa khoảng [ 1 ; + ∞ ) ?
A. - ∞ ; - 14 15
B. ( - ∞ ; - 14 15 ]
C. - 2 ; - 14 15
D. [ - 14 15 ; + ∞ )
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x - m + 2 x + 1 giảm trên các khoảng mà nó xác định ?
A. m < - 3.
B. m ≤ - 3.
C. m ≤ 1.
D. m < 1 .
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x - m + 2 x + 1 giảm trên các khoảng mà nó xác định ?
A. m < 1
B. m ≤ -3
C. m ≤ 1
D. m < -3
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x - m + 2 x + 1 giảm trên các khoảng mà nó xác định ?
A. m<-3
B. m ≤ -3
C. m ≤ 1
D. m < 1
Cho hàm số y = f(x) xác định trên R\{2}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ:
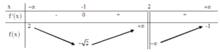
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f(x) = m có 3 nghiệm thực phân biệt.
![]()
![]()
![]()
![]()
Cho hàm số f ( x ) = 5 x - 1 - 2 x - 1 k h i x > 1 m x + m + 1 4 k h i x ≤ 1 (m là tham số). Giá trị của m để hàm số liên tục trên R là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Cho hàm số f ( x ) = x + 4 - 2 x k h i x > 0 m x 2 + 2 m + 1 4 k h i x ≤ 0 , m là tham số. Tìm giá trị của m để hàm số liên tục tại x=0.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) có đạo hàm trên khoảng 0 ; + ∞ và f(x)>0, ∀ x ∈ 0 ; + ∞ thỏa mãn f ' x = - x . f 2 x ∀ x ∈ 0 ; + ∞ , biết f 1 = 2 a + 3 và f 2 > 1 4 . Tổng tất cả các giá trị nguyên của a thỏa mãn là
A. -14.
B. 1.
C. 0.
D. -2.