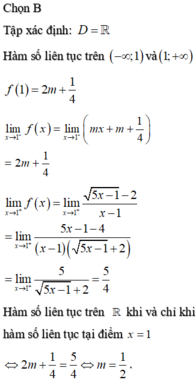Các câu hỏi tương tự
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2) 1 và
∫
1
2
F
(
x
)
d
x
5
. Tính I
∫
1
2
(
x
-
1
)
f
(
x
)
d
x
Đọc tiếp
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2) = 1 và ∫ 1 2 F ( x ) d x = 5 . Tính I= ∫ 1 2 ( x - 1 ) f ( x ) d x
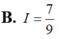
![]()
![]()
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2)1 và
∫
1
2
F
(
x
)
d
x
5
. Tính
I
∫
1
2
(
x
-
1
)
f
(
x
)
d
x
Đọc tiếp
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2)=1 và ∫ 1 2 F ( x ) d x = 5 . Tính I = ∫ 1 2 ( x - 1 ) f ( x ) d x
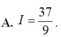
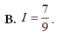
![]()
![]()
Biết hàm số yf(x) có
f
(
x
)
3
x
2
+
2
x
-
m
+
1
,
f
(
2
)
1
và đồ thị của hàm số yf(x) cắt trục tung tại điểm có tung độ bằng -5. Hàm số f(x) là:
Đọc tiếp
Biết hàm số y=f(x) có f ' ( x ) = 3 x 2 + 2 x - m + 1 , f ( 2 ) = 1 và đồ thị của hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng -5. Hàm số f(x) là:
![]()
![]()
![]()
![]()
Biết hàm số yf(x) có
f
(
x
)
3
x
2
+
2
x
-
m
+
1
, f(2)1 và đồ thị của hàm số yf(x) cắt trục tung tại điểm có tung độ bằng –5. Hàm số f(x) là
Đọc tiếp
Biết hàm số y=f(x) có f ' ( x ) = 3 x 2 + 2 x - m + 1 , f(2)=1 và đồ thị của hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng –5. Hàm số f(x) là
![]()
![]()
![]()
![]()
Cho hàm số
y
f
(
x
)
liên tục trên R và có đạo hàm
f
(
x
)
x
2
(
x
-
2
)
(
x
2
-
6
x
+
m
)
, với mọi
x
∈
R
. Có bao nhiêu số nguyên m thuộc đoạn
-
2019
;
2019
để...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = x 2 ( x - 2 ) ( x 2 - 6 x + m ) , với mọi x ∈ R . Có bao nhiêu số nguyên m thuộc đoạn - 2019 ; 2019 để hàm số g ( x ) = f ( 1 - x ) nghịch biến trên khoảng - ∞ ; - 1
A. 2012
B. 2011
C. 2009
D. 2010
Cho hàm số f(x) = (x2-m)/(x-1) (m ≠ 1)
A,y = x4 – 2x2 – 5.
B,Hàm số luôn giảm trên tập xác định.
C,Hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1.
D,Hàm số luôn tăng trên (-∞;1) và (1;+∞).
Cho hàm số
f
(
x
)
2
x
2
-
3
x
+
1...
Đọc tiếp
Cho hàm số f ( x ) = 2 x 2 - 3 x + 1 2 ( x - 1 ) k h i x ≠ 1 m k h i x = 1 . Tìm m để hàm số f(x) liên tục tại x=1.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số
f
x
1
1
+
sinx
a) F(x) 1 -
cos
x
2
+
π
4...
Đọc tiếp
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
Cho hàm số yf(x) có đạo hàm f(x)
(
x
2
-
1
)
(
x
-
2
)
. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
f
(
x
2
+
m
)
có 5 điểm cực trị. Số phần tử của tập S là. A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số
f
(
x
)
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3...
Đọc tiếp
Cho hàm số
f
(
x
)
=
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
,
với m là tham số thực.
Hàm số
g
(
x
)
=
x
2
+
4
x
+
5
x
+
2
có đồ thị C và bảng biến thiên sau:
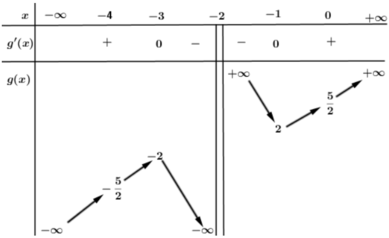
Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1
A. m> 2
B. 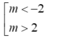
C. m < -5/2
D. m> 5 2