Cho một cấp số cộng u n có u 1 = 5 và tổng 50 số hạng đầu bằng 5150. Tìm công thức của số hạng tổng quát u n
A. u n = 1 + 4 n
B. u n = 5 n
C. u n = 3 + 2 n
D. u n = 2 + 3 n
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
A. n = 79
B. n = 78
C. n = 77
D. n = 80
Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
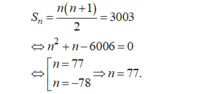
Cho một cấp số cộng u n c ó u 1 = 5 và tổng 40 số hạng đầu bằng 3320. Tìm công sai của cấp số cộng đó.
A. 4
B. -4
C. 8
D. -8
Một cấp số cộng cố số hạng đầu bằng 5 và công sai bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng 2700?
Ta có: \({S_n} = \frac{n}{2}\left[ {2 \times 5 + \left( {n - 1} \right) \times 2} \right] = 2700\;\)
\( \Leftrightarrow \frac{n}{2}\left( {8 + 2n} \right) = 2700\;\)
\( \Leftrightarrow {n^2} + 4n - 2700 = 0\;\)
\( \Leftrightarrow \left[ \begin{array}{l}n = - 54(L)\\n = 50(TM)\end{array} \right.\)
Vậy phải lấy tổng 50 số hạng đầu
Một cấp số cộng có tổng n số hạng đầu S n được tính theo công thức S n = 5 n 2 + 3 n , ( n ∈ N * ) . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó
A. u 1 = - 8 , d = 10
B. u 1 = - 8 , d = - 10
C. u 1 = 8 , d = 10
D. u 1 = 8 , d = - 10
Một cấp số cộng có tổng n số hạng đầu S n được tính theo công thức S n = 5 n 2 + 3 n , ( n ∈ N * ) . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó
A. u 1 = - 8 , d = 10
B. u 1 = - 8 , d = - 10
C. u 1 = 8 , d = 10
D. u 1 = 8 , d = - 10
Một cấp số cộng có tổng của n số hạng đầu S n tính theo công thức S n = 5 n 2 + 3 n n ∈ N * . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó.
A. u 1 = - 8 , d = 10
B. u 1 = - 8 , d = - 10
C. u 1 = 8 , d = 10
D. u 1 = 8 , d = - 10
Một cấp số cộng có tổng của n số hạng đầu S n tính theo công thức S n = 5 n 2 + 3 n , ( n ∈ ℕ * ) . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó
A. u 1 = - 8 ; d = 10 .
B. u 1 = - 8 ; d = - 10 .
C. u 1 = 8 ; d = 10 .
D. u 1 = 8 ; d = - 10 .
