hàm số f ( x ) = ln 1 - 1 x 2 . Biết rằng f ( 2 ) + F ( 3 ) + . . . + f ( 2018 ) = ln a - ln b + ln c - ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a<b<c<d. Tính P=a+b+c+d
A. 1986
B. 1698
C. 1689
D. 1968
Cho hàm số f(x)=ln2018-ln(x+1 / x).Tính S=f’(1)+f’(2)+f’(3)+…+f’(2017)
A. 4035 2018
B. 2017
C. 2016 2017
D. 2017 2018
Cho hàm số f ( x ) = ln 2019 - ln x + 2 x tính tổng S = f ' ( 1 ) + f ' ( 3 ) + . . . + f ' ( 2019 )
A. 4305 2019
B. 2021
C. 2019 2021
D. 2020 2021
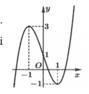
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
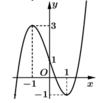
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Bất phương trình m > f(x) - ln(-x) đúng với mọi x ∈ - 1 ; - 1 e
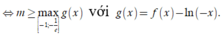
Ta có ![]()
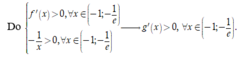
Suy ra hàm số g(x) đồng biến trên ![]()
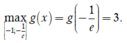
Chọn D.
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f - 1 = 1 ; f - 1 e = 2 . Bất phương trình f x < ln - x + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
a) F(x) = 1 - cos x 2 + π 4
d) K(x) = 2 1 - 1 1 + tan x 2
Tính đạo hàm cấp hai của mỗi hàm số sau:
a) \(y = 2{x^4} - 3{x^3} + 5{x^2}\)
b) \(y = \frac{2}{{3 - x}}\)
c) \(y = \sin 2x\cos x\)
d) \(y = {e^{ - 2x + 3}}\)
e) \(y = \ln (x + 1)\)
f) \(y = \ln ({e^x} + 1)\)
\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)
e,
\(y = \ln (x + 1) \Rightarrow y' = \frac{1}{{x + 1}} \Rightarrow y'' = - \frac{1}{{{{\left( {x + 1} \right)}^2}}}\)
f,
\(y = \ln ({e^x} + 1) \Rightarrow y' = \frac{{{e^x}}}{{{e^x} + 1}} \Rightarrow y'' = - \frac{{{e^x}.{e^x}}}{{{{\left( {{e^x} + 1} \right)}^2}}} = - \frac{{{e^{2x}}}}{{{{\left( {{e^x} + 1} \right)}^2}}}\)
Họ nguyên hàm của hàm số f(x) = 4x(1+ln x) là
A. 2 x 2 ln x + 3 x 2
B. 2 x 2 ln x + x 2
C. 2 x 2 ln x + 3 x 2 + C
D. 2 x 2 ln x + x 2 + C
Đáp án D
Phương pháp:
Cách 1: Sử dụng công thức tính nguyên hàm của 1 tổng.
Cách 2: Đạo hàm từng đáp án của đề bài, kết quả nào ra đúng f(x) thì đó là đáp án đúng
Cách giải:
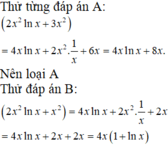
⇒ 2 x 2 ln x + x 2 là một nguyên hàm của hàm số f x = 4 x 1 + ln x
⇒ Họ nguyên hàm của hàm số f x = 4 x 1 + ln x là 2 x 2 ln x + x 2 + C
Họ các nguyên hàm của hàm số f(x) = (2x + 1) ln x là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = ln 2 x + 1 . ln x x thoả mãn F ( 1 ) = 1 3 . Giá trị của F 2 ( e ) là
A. 8 9
B. 1 9
C. 8 3
D. 1 3
Chọn A
Đặt t = ln 2 x + 1 ⇒ t 2 = ln 2 x + 1 ⇒ t d t = ln x x d x
∫ ln 2 x + 1 . ln x x d x = ∫ t 2 d t = t 3 3 + C = ln 2 x + 1 3 3 + C
Vì F ( 1 ) = 1 3 nên C = 0
Vậy F 2 ( e ) = 8 9
CMR \(F\left(x\right)=ln\dfrac{x^2-x\sqrt{2}+1}{x^2+x\sqrt{2}+1}\) là 1 nguyên hàm của hàm số \(f\left(x\right)=\dfrac{2\sqrt{2}\left(x^2-1\right)}{x^4+1}\) tren R
Cíu iem với anh Lâm ơi, 2 cách nhé anh :3
Làm xuôi thì đơn giản, tính \(F'\left(x\right)\) là xong (chịu khó biến đổi)
Làm ngược thì nhìn biểu thức hơi thiếu thân thiện
\(\int\dfrac{2\sqrt{2}\left(x^2-1\right)}{x^4+1}dx=\int\dfrac{2\sqrt{2}\left(x^2-1\right)}{\left(x^2-x\sqrt{2}+1\right)\left(x^2+x\sqrt{2}+1\right)}dx\)
Phân tách hệ số bất định:
\(\dfrac{2\sqrt{2}\left(x^2-1\right)}{\left(x^2-x\sqrt{2}+1\right)\left(x^2+x\sqrt{2}+1\right)}=\dfrac{a\left(2x-\sqrt{2}\right)}{x^2-x\sqrt{2}+1}+\dfrac{b\left(2x+\sqrt{2}\right)}{x^2+x\sqrt{2}+1}\)
Quan tâm tử số: \(a\left(2x-\sqrt{2}\right)\left(x^2+x\sqrt{2}+1\right)+b\left(2x+\sqrt{2}\right)\left(x^2-x\sqrt{2}+1\right)\)
\(=2\left(a+b\right)x^3+\sqrt{2}\left(a-b\right)x^2+\sqrt{2}\left(b-a\right)\)
Đồng nhất 2 tử số: \(\left\{{}\begin{matrix}a+b=0\\a-b=2\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\end{matrix}\right.\)
Do đó:
\(\dfrac{2\sqrt{2}\left(x^2-1\right)}{x^4+1}=\dfrac{2x-\sqrt{2}}{x^2-x\sqrt{2}+1}-\dfrac{2x+\sqrt{2}}{x^2+x\sqrt{2}+1}\)