Cho ∫ 0 π f ( x ) d x = 2 và ∫ 0 π g ( x ) d x = - 1 . Tính I= ∫ 0 π ( 2 f ( x ) + x sin x - 3 g ( x ) ) d x
![]()
![]()
![]()
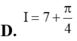
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Cho hàm số f(x) = sin3x.
Tính f''(-π/2), f''(0), f''(π/18)
f''(-π/2) = -9, f''(0) = 0, f''(π/18) = -9/2
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
![]()
![]()
![]()
![]()
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
A. f ( π ) = 0
B. f ( π ) = - π
C. f ( π ) = 4 π
D. f ( π ) = 2 π
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
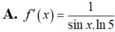
![]()
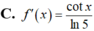
![]()
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;π/4] thỏa mãn f(0)=0, ∫ 0 π 4 f ' x 2 d x = 2 và ∫ 0 π 4 sin 2 x f ( x ) d x = 1 2 Tích phân ∫ 0 π 4 f x d x bằng
A. -1/2
B. 1/2
C. -1/4
D. 1/4
Cho hàm số f(x) có đạo hàm liên tục trên 0 ; π . Biết f 0 = 2 e và f(x) luôn thỏa mãn đẳng thức f ' x + sinx . f x = cosx . e cosx , ∀ x ∈ 0 ; π . Tính I = ∫ 0 π f x dx (làm tròn đến phần trăm).
A. I ≈ 6,55
B. I ≈ 17,30
C. I ≈ 10,31
D. I ≈ 16,91
Cho hình phẳng H giới hạn bởi các đường: y = f(x), y = 0, x = b và x = a (trong đó hàm số f(x) liên tục trên đoạn [b,a]). Thể tích khối tròn xoay tạo nên bởi phép quay H quanh trục Ox được cho bởi công thức:
A. π ∫ a b f 2 x d x B. ∫ a b f 2 x d x
C. π ∫ b a f 2 x d x D. ∫ b a π f x 2 d x
Đáp án: C.
Lưu ý ở đây b là cận dưới còn a là cận trên (b ≤ a), vậy A sai, B thiếu hệ số π , D có hệ số π 2
Cho hàm số f(x) thỏa mãn ∫ 0 π f ' ( x ) d x = 1 , f ( 0 ) = π . Tính f ( π )
A. f ( π ) = 1 - π
B. f ( π ) = π - 1
C. f π = π + 1
D. f π = - π - 1
Có f ( π ) - f ( 0 ) = ∫ 0 π f ' ( x ) dx
f ( π ) = f ( 0 ) + ∫ 0 π f ' ( x ) dx = π + 1
Chọn đáp án C.
Câu 1 : Tính thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y = x3 , y = 0, x=0, x=1 quanh trục hoành
Câu 2 : Biết F(x) là một nguyên hàm của hàm f(x) = sin2x và F(π/4) = 1. Tính F(π/6)
1.
\(V=\pi\int\limits^1_0x^6dx=\dfrac{\pi x^7}{7}|^1_0=\dfrac{\pi}{7}\)
2.
\(F\left(x\right)=\int sin2xdx=-\dfrac{1}{2}cos2x+C\)
\(f\left(\dfrac{\pi}{4}\right)=1\Leftrightarrow-\dfrac{1}{2}cos\dfrac{\pi}{2}+C=1\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}cos2x+1\Rightarrow F\left(\dfrac{\pi}{6}\right)=\dfrac{3}{4}\)