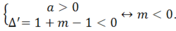Tìm tất cả các giá trị thực của tham số m để hàm số y = m log 2 x - 2 log 2 x - m - 1  nghịch biến trên (4;+¥).

A. m < -2 hoặc m >1.

B. m £ -2 hoặc m =1.

C. m < -2 hoặc m =1.

D. m < -2.

Tìm tất cả các giá trị thực của tham số m để hàm số  y = sin 3 x - 3 cos 2 x - msinx - 1 đồng biến trên đoạn π ; 3 π 2 .

A. m ³ -3 .

B. m ³ 0 . 

C. m £ -3 .

D. m £ 0 .

Tìm tất cả các giá trị thực của tham số m để hàm số  y = sin 3 x - 3 cos 2 x - m sin x - 1 đồng biến trên đoạn  π ; 3 π 2

A.  m ≥ - 3

B.  m ≥ 0

C.  m ≤ - 3

D.  m ≤ 0

Cho hàm số  y = f x = x 3 - 2 m + 1 x 2 + 3 - m x + 2 . Tìm tất cả các giá trị của tham số m để hàm số y = f x  có 3 điểm cực trị.

A. m ³ 3

B. m > 3

C.  - 1 2 < m  

D.  m < - 1 2

Tìm tất cả các giá trị của tham số m để hàm số  y = - x 3 + m x 2 - x có 2 điểm cực trị

A.  | m | ≥ 2 3

B.  | m | > 2

C.  | m | > 3

D.  | m | ≥ 3

Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:

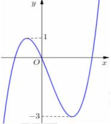
A.  m ≤ - 1 hoặc  m ≥ 3

B.  m ≤ - 3 hoặc  m ≥ 1

C. m = -1 hoặc m = 3

D.  1 ≤ m ≤ 3

Cho hàm số y = f x = x + 3 m - 2 y. Tất cả các giá trị của tham số m sao cho f x ≥ 0 , ∀ x ∈ [ 1 ; + ∞ )  là

A.  m ≤ 1 3

B.  m ≤ 2 3

C.  m ≥ 1 3

D.  0 < m ≤ 2 3

Cho hàm số y = f x = m 2 - 1 x + 2 m - 3 .

Tất cả các giá trị của tham số m để hàm số đồng biến trên ℝ  là

A.  m > 3 2

B. -1 < m < 1

C.  [ m < - 1 m > 1

D.  m ≠ ± 1