Cho đồ thị C : y = 4 x 3 - 3 x + 1 và đường thẳng d : y = m ( x - 1 ) + 2 . Tất cả giá trị tham số m để (C) cắt d tại một điểm là
A. m = 9
B. m ≤ 0
C. m ≤ 0 hoặc m = 9
D. m < 0
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Cho hàm số \(y=\left(m-1\right)x-4\) có đồ thị là đường thẳng (d).
a) Vẽ đồ thị hàm số trên khi \(m=3\)
b) Tìm m để đường thẳng (d) song song với đường thẳng \(y=-3x+2\)
c) Tìm m để đường thẳng (d) cắt đồ thị hàm số \(y=x-7\) tại một điểm nằm bên trái trục tung
b: Để (d)//y=-3x+2 thì m-1=-3
=>m=-2
c:
PTHĐGĐ là:
(m-1)x-4=x-7
=>(m-2)x=-3
Để hai đường cắt nhau tại một điểm nằm bên trái trục tung thì m-1<>1 và -3/(m-2)<0
=>m<>2 và m-2>0
=>m>2
Cho hàm số bậc nhất y=(m+1)x-3 có đồ thị hàm số là đường thẳng d (m là tham số, m khác -1)
a) Tìm m để (d) đi qua E(4; 1) và vẽ đồ thị hàm số với m tìm được.
b) Cho (d’): y=5x-8 . Tìm m để (d) ⊥(d’).
c) Tìm m để đường thẳng (d) cắt đường thẳng y=3x-1 tại điểm có hoành độ bằng 2, tìm tọa độ giao điểm.
d) Xác định m để (d) cắt hai trục Ox, Oy tại A và B sao cho tam giác AOB có diện tích bằng 2 (đơn vị diện tích).
a: Thay x=4 và y=1 vào y=(m+1)x-3, ta được:
4(m+1)-3=1
=>4m+4-3=1
=>4m+1=1
hay m=0
b: Để hai đường vuông góc thì 5(m+1)=-1
=>m+1=-1/5
hay m=-6/5
c: Thay x=2 vào y=3x-1, ta được:
\(y=3\cdot2-1=5\)
Thay x=2 và y=5 vào (d), ta được:
2(m+1)-3=5
=>2(m+1)=8
=>m+1=4
hay m=3
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C) , đường thẳng (d): y=m(x+1) với m là tham số, đường thẳng ∆ : y = 2 x - 7 . Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với ∆ và d B ; ∆ + d C ; ∆ = 6 5 .
A. 0
B. 8
C. 5
D. 4
Cho hàm số y = x 3 - 3 x 2 + 3 có đồ thị (C) và đường thẳng d : y = x + 3 . Số giao điểm của đường thẳng d với đồ thị (C) bằng bao nhiêu?
A. 0.
B. 2.
C. 1.
D. 3.
Bài 2: Cho hàm số y = - x + 3 có đồ thị (d) a) Vẽ (d) b) Tính góc tạo bởi đường thẳng y = - x + 3 với trục hoành c) Xác định hàm số y = ax+b biết đồ thị của nó song song với đường thẳng (d) và qua điểm (4;2)
Bài 3: Cho tam giác ABC nội tiếp đường tròn (O;R) đường kính BC. Gọi H là trung điểm của AC. Tia OH cắt đường tròn (O) tại điểm M. Từ A vẽ tia tiếp tuyến Ax với đường tròn (O) cắt tia OM tại N a/ Chứng minh : OM // AB b/ Chứng minh: CN là tiếp tuyến của đường tròn (O) c) Giả sử góc B có số đo bằng 600 . Tính diện tích của tam giác ANC.
Bài 2:
c: Vì (d')//(d) nên a=-1
Vậy: (d'): y=-x+b
Thay x=4 và y=2 vào (d'), ta được:
b-4=2
hay b=6
Cho hàm số : y=x-4 có đồ thị là (d)
a) Vẽ đồ thị (d) của hàm số đã cho
b) Tìm giá trị của a để đồ thị hàm số y=(3-a)x+1 // d
c) Chứng minh: đường thẳng y = mx+2 .(m+1) (d') luôn đi qua một điểm cố định thuộc đường thẳng (d)
b: Để hai đường song song thì 3-a=1
hay a=2
c: Phương trình hoành độ giao điểm là:
\(mx+2\left(m+1\right)=x-4\)
\(\Leftrightarrow mx-x=-4-2m-2\)
\(\Leftrightarrow x\left(m-1\right)=-2m-6\)
KHi m<>1 thì \(x=\dfrac{-2m-6}{m-1}\) luôn thuộc (d)
=>ĐPCM
cho đường thẳng d y= -x+m và đồ thị y= x+2/x+1. Tìm m để đường thẳng d và đồ thị không có điểm chung
Phương trình hoành độ giao điểm:
\(\dfrac{x+2}{x+1}=-x+m\Rightarrow x+2=\left(x+1\right)\left(-x+m\right)\)
\(\Rightarrow x^2+\left(2-m\right)x-m+2=0\) (1)
d và (C) không có điểm chung khi (1) vô nghiệm
\(\Rightarrow\Delta=\left(2-m\right)^2-4\left(-m+2\right)< 0\)
\(\Rightarrow-2< m< 2\)
Cho hàn số bậc nhất y=(m+1)x+m-2 có đồ thị là (d)
1.Tìm m để hàm số đã cho đồng biến ; ngịch biến trên R
2.Tìm m biết đồ thị (d) đi qua điểm M(-1;-2)
3.Biết đồ thị (d) cắt trục tung tại điểm có tung độ bằng 2020. Tìm m ?
4.Biết đồ thị (d) cắt trục hoành tại điểm có hoành độ bằng 10 . Tìm m ?
5.Biết đồ thị (d) song song với đường thẳng y=1-2x. Tìm m ?
6.Biết đồ thị (d) cắt đường thẳng y= -x-1 tại điểm có tung độ là 1. Tìm m?
7.Biết đồ thị (d) cắt đường thẳng y= -x-1 tại điểm có hoành độ là 1. Tìm m?
8.Biết đồ thị (d) và đường thẳng y=2x-3 . Biết đồ thị (d) cắt đường thẳng tại điểm nằm trên trục tung .Tìm m ?
9.Biết đồ thị (d) và đường thẳng y=2x-3 . Biết đồ thị (d) cắt đường thẳng tại điểm nằm trên trục hoành .Tìm m ?
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
y = − x 3 + 3x + 1
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:
y = ( x + 1 ) 3 − 3x − 4
c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
( x + 1 ) 3 = 3x + m
d) Viết phương trình tiếp tuyến (d) của đồ thị (C’), biết tiếp tuyến đó vuông góc với đường thẳng
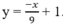
a)
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
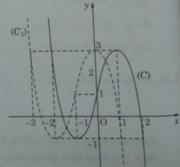
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
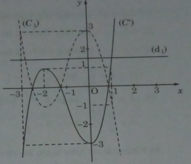
d) Vì (d) vuông góc với đường thẳng:
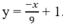
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 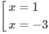
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.