Đường đẳng nhiệt trong hệ trục tọa độ (OpV) là
A. một đường thẳng song song với trục OV.
B. một đường Hypebol.
C. một đường thẳng nếu kéo dài thì đi qua gốc tọa độ.
D. một đường thẳng song song với trục OP.
Trong hệ tọa độ (V, T), đường biểu diễn nào sau đây là đường đẳng áp?
A. Đường thẳng song song với trục hoành
B. Đường thẳng song song với trục tung
C. Đường hypebol
D. Đường thẳng kéo dài đi qua gốc tọa độ.
Trong hệ tọa độ (V, T), đường biểu diễn nào sau đây là đường đẳng áp?
A. Đường thẳng song song với trục hoành
B. Đường thẳng song song với trục tung
C. Đường hypebol
D. Đường thẳng kéo dài đi qua gốc tọa độ.
Trong hệ tọa độ (p, T), đường biểu diễn nào sau đây là đường đẳng tích?
A. Đường hypebol
B. Đường thẳng kéo dài qua gốc tọa độ
C. Đường thẳng không đi qua gốc tọa độ
D. Đường thẳng cắt trục p tại điểm p = po
Trong hệ tọa độ (p, T), đường biểu diễn nào sau đây là đường đẳng tích?
A. Đường hypebol
B. Đường thẳng kéo dài qua gốc tọa độ
C. Đường thẳng không đi qua gốc tọa độ
D. Đường thẳng cắt trục p tại điểm p = po
Trong hệ tọa độ (p, T), đường biểu diễn nào sau đây là đường đẳng tích?
A. Đường hypebol
B. Đường thẳng kéo dài qua gốc tọa độ
C. Đường thẳng không đi qua gốc tọa độ
D. Đường thẳng cắt trục p tại điểm p = po
Cho hàm số y = 2 x + 1 x − 1 có đồ thị là (H) và đường thẳng d có hệ số góc m và đi qua điểm A − 2 ; 2 . Giả sử d cắt (H) tại hai điểm phân biệt M, N. Qua M kẻ các đường thẳng lần lượt song song với các trục tọa độ, qua N kẻ các đường thẳng lần lượt song song với các trục tọa độ. Tìm số các giá trị thực của tham số m sao cho bốn đường thẳng đó tạo thành một hình vuông.
A. 0
B. 1
C. 2
D. 3
Đáp án B.
Phương trình đường thẳng d : y = m x + 2 + 2 .
Phương trình hoành độ giao điểm của và d:
2 x + 1 x − 1 = m x + 2 + 2 ⇒ m x 2 + m x − 2 m − 3 = 0 (*).
Để (H) và d cắt nhau tại hai điểm phân biệt thì (*) phải có hai nghiệm phân biệt ⇔ m ≠ 0 Δ > 0 ⇔ m ≠ 0 9 m 2 + 12 > 0 (**). Gọi là hai nghiệm của (*).
Khi đó M = x 1 ; m x 1 + 2 + 2 , N = x 2 ; m x 2 + 2 + 2 .
Hai cạnh của hình chữ nhật tạo bởi bốn đường thẳng như đã cho trong bài là x 2 − x 1 và m x 2 − x 1 . Hình chữ nhật này là hình vuông khi và chỉ khi m x 2 − x 1 = x 2 − x 1 ⇔ m = 1 ⇔ m = ± 1 . Ta thấy chỉ có M=1 thỏa mãn (**).
Vậy chỉ có một giá trị của m thỏa mãn yêu cầu bài toán. Chọn đáp án B.
cho hàm số đường thẳng y = (2m - 1) x + m. tìm m để...........................................................a) đường thẳng đi qua gốc tọa độ.....b) đường thẳng cắt trục tung tại điểm có tung độ bằng -2....c. đường thẳng song song với đường thẳng y = x - 5.
a) Thay x=0 và y=0 vào (d), ta được:
\(\left(2m-1\right)\cdot0+m=0\)
\(\Leftrightarrow m=0\)
b) Thay x=0 và y=2 vào (d), ta được:
\(\left(2m-1\right)\cdot0+m=2\)
\(\Leftrightarrow m=2\)
c) Để (d)//y=x-5 thì \(\left\{{}\begin{matrix}2m-1=1\\m\ne-5\end{matrix}\right.\Leftrightarrow m=1\)
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x 2 = y − 1 2 = z − 1 và điểm A(1;0;0). Viết phương trình đường thẳng đi qua A và song song với đường thẳng d.
A. x − 1 1 = y 1 = z 4
B. x + 1 1 = y 1 = z 4
C. x + 1 2 = y 2 = z − 1
D. x − 1 2 = y 2 = z − 1
Vẽ qua điểm B(0; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)
Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
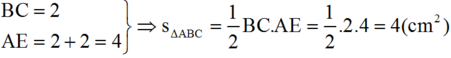
Trong mặt phẳng tọa độ Oxy cho 3 điểm A(-5;-1) B(-1;4) và C(3;2)
a.vẽ tam giác ABC
b.viết phương trình đường thẳng BC
c.không dùng đồ thị ,hãy xác định tọa độ của điểm D với D là giao điểm của đường thẳng qua A song song với BC và đường thẳng qua B song song với trục Oy
(ý c điều kiện để đường thẳng song song với trục tung là gì ạ)
Ta thấy trục tung có phương trình : x = 0.
Như vậy điều kiện để một đường thẳng song song với trục tung là nó có phương trình: x = a, với a là một hằng số.
Em hãy thử làm tiếp nhé :))
Trong không gian với hệ trục tọa độ Oxyz, phương trình đường thẳng đi qua A − 1 ; 0 ; 1 và song song với trục Oy
A. x = − 1 + t y = 0 z = 1 + t , t ∈ ℝ
B. x = − 1 y = t z = 1 , t ∈ ℝ
C. x = − t y = 1 z = t , t ∈ ℝ
D. x = − 1 y = 1 + t z = 1 , t ∈ ℝ