Cho hình chóp S.ABC có S A ⊥ ( A B C ) ,   A B = 1 ,   A C = 2 ,   B A C ^ = 60 °  Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu đi qua các điểm A,B,C,M,N

Cho hình chóp S.ABCD có SA ^ (ABC), AB = 1, AC = 2 và  B A C   ^ = 60 ∘ .

Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của

mặt cầu đi qua các điểm A, B, C, M, N.

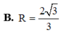
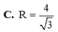
Cho hình chóp S.ABC có SA vuông góc với (ABC), AB=a, AC=a 2 , B A C ^ = 45 ° . Gọi B',C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A.BCC'B'.

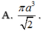
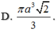
Cho hình chóp S.ABC có cạnh S A ⊥ A B C , tam giác ABC đều và A B = a ; góc giữa SB và mặt phẳng (ABC) bằng 60 o . Gọi M,N lần lượt là trung điểm của SA,SB. Tính thể tích khối chóp S . M N C :

A.  a 3 16

B.  a 3 4

C.  a 3 3 12

D.  a 3 8

Cho hình chóp S.ABC có S A ⊥ A B C , tam giác ABC đều AB = a; góc giữa SB và mặt phẳng (ABC) bằng 60 o . Gọi M,N lần lượt là trung điểm của SA,SB. Tính thể tích khối chóp S.MNC:   

A.  a 3 16

B.  a 3 4

C.  a 3 3 12

D.  a 3 8

Cho hình chóp S.ABC có S A ⊥ ( A B C ) , AC = b, AB = c, . Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c, α .

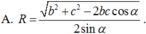
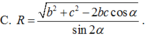
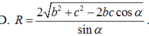
Cho hình chóp S.ABC  có đáy ABC là tam giác vuông cân có AB = BC = a. Cạnh bên SA vuông góc với đáy,  góc SBA = 60°. Gọi M là điểm nằm trên AC sao cho A C → = 2 C M → . Tính khoảng cách giữaSM và AB.

A.  6 a 7 7

B.  a 7 7

C.  a 7 21

D.  3 a 7 7