Tìm hệ số của số hạng chứa x 15 trong khai triển ( 2 x 3 - 3 ) n thành đa thức, biết n là số nguyên dương thỏa mãn hệ thức A n 3 + C n 1 = 8 C n 2 + 49
A. 6048
B. 6480
C. 6408
D. 4608
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
Trong khai triển nhị thức x + 1 x n , x ≠ 0 , hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức x + 1 x n , x ≠ 0 hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
a)Tìm số hạng không chứa x trong khai triển (x+2/x)10
b)Tìm số hạng không chứa x trong khai triển (x+2/x2)6
c)Tìm hệ số của số hạng chứa x10 trong khai triển (3x3-2/x2)5
a: SHTQ là: \(C^k_{10}\cdot x^{10-k}\cdot\left(\dfrac{2}{x}\right)^k=C^k_{10}\cdot2^k\cdot x^{10-2k}\)
Số hạng ko chứa x tương ứng với 10-2k=0
=>k=5
=>SH đó là 8064
b: SHTQ là; \(C^k_6\cdot x^{6-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_6\cdot2^k\cdot x^{6-3k}\)
Số hạng ko chứa x tương ứng với 6-3k=0
=>k=2
=>Số hạng đó là 60
c: SHTQ là: \(C^k_5\cdot\left(3x^3\right)^{5-k}\cdot\left(-\dfrac{2}{x^2}\right)^k\)
\(=C^k_5\cdot3^{5-k}\cdot\left(-2\right)^k\cdot x^{15-5k}\)
SH chứa x^10 tương ứng với 15-5k=10
=>k=1
=>Hệ số là -810
Tìm hệ số của số hạng chứa x^10 trong khai triển: (x^2-x^3+1)^10
\(\left(x^2-x^3+1\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(x^2-x^3\right)^k=\sum\limits^{10}_{k=0}C_{10}^k\sum\limits^k_{i=0}C_k^i.\left(x^2\right)^i.\left(-x^3\right)^{k-i}\)
\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^k.C_k^i.\left(-1\right)^{k-i}.x^{3k-i}\)
Số hạng chứa \(x^{10}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le k\le0\\0\le i\le k\\3k-i=10\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(2;4\right);\left(5;5\right)\)
\(\Rightarrow\) Hệ số: \(C_{10}^4.C_4^2+C_{10}^5.C_5^5=...\)
Tìm hệ số của x 4 trong khai triển 1 + 2 x n . Biết rằng hệ số của số hạng chứa x 2 gấp 3 lần hệ số của số hạng chứa x.
A. 4
B. 6
C. 8
D. 16
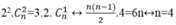
Hệ số của x4 trong khai triển (1+2x)4 là 24 =16
Chọn D
8. Trong khai triển (8a^2 - 1/2b)^6 hệ số của số hạng chứa a^9.b^3 là?
9. Trong khai triển ( x + 8/x^2)^9 số hạng ko chứa x là?
A. 4308
B. 86016
C. 84
D. 43008
Câu 8 là \(\left(8a^2-\dfrac{1}{2}b\right)^6\) hay \(\left(8a^2-\dfrac{1}{2b}\right)^6\) bạn? (tốt nhất là bạn dùng tính năng gõ công thức toán để đăng đề, hoặc chụp hình gửi đề trực tiếp lên, hiện nay hoc24 đã cho đăng đề bằng hình ảnh)
9.
\(\left(x+8.x^{-2}\right)^9=\sum\limits^9_{k=0}C_9^kx^{9-k}.8^k.x^{-2k}=\sum\limits^9_{k=0}C_9^k8^kx^{9-3k}\)
Số hạng ko chứa x \(\Rightarrow9-3k=0\Rightarrow k=3\)
Số hạng đó là: \(C_9^3.8^3=...\)
Biết tổng các hệ số của khai triển \(\left(3-x^2\right)^n\)bằng 1024. Hệ số của số hạng chứa \(x^{12}\) trong khai triển đó bằng bao nhiêu?
\(\left(3-1\right)^n=1024\Leftrightarrow2^n=2^{10}\Rightarrow n=10\)
\(\left(3-x^2\right)^{10}\) có SHTQ: \(C_{10}^k.3^k.\left(-1\right)^{10-k}.x^{20-2k}\)
Số hạng chứa \(x^{12}\Rightarrow20-2k=12\Rightarrow k=4\)
Hệ số: \(C_{10}^4.3^4=...\)
Tìm hệ số của số hạng không chứa x trong khai triển x - 1 x n . Biết có đẳng thức là:
C n 2 C n n - 2 + 2 C n 2 C n 3 + C n 3 C n n - 3 = 100
A. 9
B. 8
C. 6
D. 7