https://video.vietjack.com/upload2/quiz_source1/2020/01/100-bai-trac-nghiem-ham-so-mu-va-logarit-co-loi-giai-chi-tiet-3-1-1579254891.PNG

bạn tham khảo nha

để pt có hai nghiệm trái dấu: 

 \(1.\left(m-10\right)< 0\\ =>m< 10\\ =>m=\left\{1;2;3;4;5;6;7;8;9\right\}\\ =>C\)

Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.

mình trình bày hơi dài mong bạn thông cảm   

Đặt \(\left|x\right|=t\ge0\)

\(\Rightarrow t^2-2t+1-m=0\) (1)

Phương trình (1) là bậc 2 nên có đối đa 2 nghiệm t

Với mỗi giá trị \(t>0\) cho 2 nghiệm x tương ứng nên pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương phân biệt

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(1-m\right)>0\\t_1+t_2=2>0\\t_1t_2=1-m>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< 1\end{matrix}\right.\) \(\Leftrightarrow0< m< 1\)

Chọn đáp án A

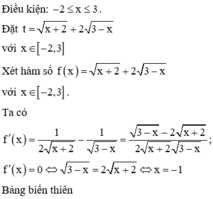
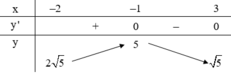
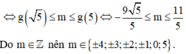
Vậy số giá trị nguyên của m để phương trình có nghiệm là 10.

Đáp án B.

Phương pháp: 

Bất phương trình m ≥ f x ,    x ∈ D có nghiệm khi và chỉ khi m ≥ M i n D f x .  

Cách giải:

ĐKXĐ:  0 < x < 1

3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x ⇔ m x − x 2 − 1 − x 1 − x ≥ x x

⇔ m ≥ x x + 1 − x 1 − x x − x 2 ,    x ∈ 0 ; 1

Để bất phương trình đã cho có nghiệm thực thì m ≥ M i n 0 ; 1 f x , f x = x x + 1 − x 1 − x x − x 2  

Xét

f x = x x + 1 − x 1 − x x − x 2 = x + 1 − x 1 − x x − 1 x x − 1 , x ∈ 0 ; 1  

Đặt t = x + 1 − x ,    t ∈ 1 ; 2  

Khi đó,  

f x = x + 1 − x 1 − x 1 − x x 1 − x = t 1 − t 2 − 1 2 t 2 − 1 2 = t 3 − t 2 t 2 − 1 = 3 t − t 3 t 2 − 1 = g t

g ' t = − t 4 − 3 t 2 − 1 2 < 0 ,     ∀ t ∈ 1 ; 2  

⇒ g t min = g 2 = 3 2 − 2 2 2 − 1 = 2 ⇒ M i n 0 ; 1 f x = 2 ⇒ m ≥ 2  

Mà

m ∈ − 9 ; 9 ⇒ m ∈ 2 ; 3 ; 4 ; ... ; 8 ⇒

Có 7 giá trị thỏa mãn.

Đáp án C.

Áp dụng bất đẳng thức Bunhiacopxki, ta có:  

m . s inx+4cosx 2 ≤ m 2 + 4 2 sin 2 x + c os 2 x = m 2 + 16.

Nên để phương trình đã cho có nghiệm   ⇔   3 m − 5 2 ≤ m 2 + 16 ⇔ 3 m 2 20 m + 9 ≤ 0.

Kết hợp với m ∈ ℤ ,  ta được m = 1 ; 2 ; 3 ; 4 ; 5 ; 6  là giá trị cần tìm.

Bảng biến thiên