Có tất cả bao nhiêu căn bậc 6 của 8
A. 2
B. Vô số
C. 0
D. 1
Những câu hỏi liên quan
Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C). Có tất cả bao nhiêu mặt cầu chứa đường tròn (C) và đi qua A?
A. 0 B. 1
C. 2 D. Vô số
Chọn B.
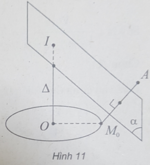
(h.11) Lấy điểm M 0 cố định trên đường tròn (C).
Gọi ( α ) là mặt phẳng trung trực của A M 0 và đường thẳng Δ là trục của (C)
Ta có: I = ( α ) ∩ ∆ là tâm mặt cầu thỏa mãn yêu cầu đề bài.
Nhận xét: Tâm I là duy nhất. Thật vậy, giả sử M nằm trên đường tròn (C) khác với M 0
Gọi ( α ') là mặt phẳng trung trực của AM và I' = ( α ') ∩ ∆
Khi đó, mặt cầu tâm I' thỏa mãn yêu cầu đề bài.
Ta có: I'A = I'M = I' M 0 cho ta I' thuộc mặt phẳng trung trực (α) của A M 0
Suy ra: I' = (α) ∩ ∆
Vậy I' ≡ I
Đúng 0
Bình luận (0)
căn bậc 2 của tất cả x+6 +căn bậc 2 tất cả của x+1 = -(x-4)(x+2)
cho 2 tập hợp A { 1 ; 9 ; 8 ; 4 } và B { 3 ; 7 ; 6 ; 5 ; 7 }a, tập hợp A có bao nhiêu phần tửb , tập hợp b có bao nhiêu phần tửc , hãy viết 1 tập hợp D có tất cả các phần tử của tập hợp A và Bd, viết tập hợp M có tất cả các số chẵn của A và B , viết cả dấu hiệu đặc trưnge , viết tập hợp G có tất cả các số lẻ của hai tập hợp , nêu dấu hiệu đặc trưngg , tạo 1 tập hợp bất kì có 2 phần tử của A và 3 phần tử của tập hơp B
Đọc tiếp
cho 2 tập hợp A = { 1 ; 9 ; 8 ; 4 } và B = { 3 ; 7 ; 6 ; 5 ; 7 }
a, tập hợp A có bao nhiêu phần tử
b , tập hợp b có bao nhiêu phần tử
c , hãy viết 1 tập hợp D có tất cả các phần tử của tập hợp A và B
d, viết tập hợp M có tất cả các số chẵn của A và B , viết cả dấu hiệu đặc trưng
e , viết tập hợp G có tất cả các số lẻ của hai tập hợp , nêu dấu hiệu đặc trưng
g , tạo 1 tập hợp bất kì có 2 phần tử của A và 3 phần tử của tập hơp B
a) Tập hợp A có 4 phần tử
b) Tập hợp B có 5 phần tử
c) \(C=\left\{1;9;8;4;3;7;6;5\right\}\)
d) \(M=\left\{4;6;8\right\}\)
\(M=\){X l X là số tự nhiên chẵn trong tập hợp A B }
e) \(G=\left\{1;9;3;7;5\right\}\)
\(G=\){ X l X là số tự nhiên lẻ trong tập hợp A B }
g) \(S=\left\{1;9;3;7;6\right\}\)
Ở tập hợp B dư 1 phân tử 7 nha ( o v o )
100 bạn nhanh nhất được k nhé
Câu 1: tìm x:
|2x - 1| = 5
Câu 2: tìm:
a) Năm bội của 4
b) Tất cả các ước của (-8)
Câu 3: cho tập hợp A = {-3;5;7}
cho tập hợp B = {-2;-1;4;9}
a) Có bao nhiêu tích x.y ( với x thuộc A, y thuộc B )?
b) Có bao nhiêu tích lớn hơn 0, bao nhiêu nhỏ hơn 0?
c) Có bao nhiêu tích là bội của 6?
d) Có bao nhiêu tích là ước của 20?
Viết đa thức trong mỗi trường hợp sau:
a) Đa thức bậc nhất có hệ số của biến bằng – 2 và hệ số tự do bằng 6;
b) Đa thức bậc hai có hệ số tự do bằng 4;
c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.
a) Đa thức bậc nhất có hệ số của biến bằng – 2 và hệ số tự do bằng 6 tức \(a = - 2;b = 6\)
\( - 2x + 6\).
b) Đa thức bậc hai có hệ số tự do bằng 4: \({x^2} + x + 4\).
c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0: \({x^4} + 0.{x^3} + {x^2} + 1 = {x^4} + {x^2} + 1\).
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0: \({x^6} + 0.{x^5} + {x^4} + 0.{x^3} + {x^2} + 0.x = {x^6} + {x^4} + {x^2}\).
Đúng 0
Bình luận (0)
Phần thực của số phức
z
2
+
3
i
200
có dạng
a
2
+
b
3
+
c
6
+
d
với a, b, c, d là các số nguyên. Trong các số a, b, c, d có tất cả bao nhiêu số bằng 0 A. 3 B. 1 C. 4 D. 2
Đọc tiếp
Phần thực của số phức z = 2 + 3 i 200 có dạng a 2 + b 3 + c 6 + d với a, b, c, d là các số nguyên. Trong các số a, b, c, d có tất cả bao nhiêu số bằng 0
A. 3
B. 1
C. 4
D. 2
Ta có 
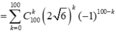
Phần thực của z tương ứng với k là bội của 2, vậy phần thực bằng
là một số nguyên dương.
Chọn đáp án A.
Đúng 0
Bình luận (0)
Phần thực của số phức
z
2
+
3
i
200
có dạng
a
2
+
b
3
+
c
6
+
d
với a, b, c, d là các số nguyên. Trong các số a, b, c, d có tất cả bao nhiêu số bằng 0. A. 3. B. 1. C....
Đọc tiếp
Phần thực của số phức z = 2 + 3 i 200 có dạng a 2 + b 3 + c 6 + d với a, b, c, d là các số nguyên. Trong các số a, b, c, d có tất cả bao nhiêu số bằng 0.
A. 3.
B. 1.
C. 4.
D. 2.
1.Tính tổng của dãy số sau :a) 4 + 8 + 12 + ........... + 200b) 12 + 18 + 24 + 30 + ................+ 3002.Tính tổng tất cả các số có hai chữ số :a) Chia hết cho 4b) Chia cho 4 dư 2c) Chia hết cho 6d) Chia cho 6 dư 5e) Chia cho 9 dư 73. Một cây cầu , ở 2 bên cầu đều có thanh lan can . Người ta đếm được tất cả có 200 thanh . Hỏi cây cầu đó dài bao nhiêu mét ? Biết rằng 2 thanh liền nhau cách nhau 2 mét .4.Một ngôi nhà 5 tầng , mỗi tầng cách nhau 4 mét . Nguwpwif ta làm bậc thang từ tầng này lên t...
Đọc tiếp
1.Tính tổng của dãy số sau :
a) 4 + 8 + 12 + ........... + 200
b) 12 + 18 + 24 + 30 + ................+ 300
2.Tính tổng tất cả các số có hai chữ số :
a) Chia hết cho 4
b) Chia cho 4 dư 2
c) Chia hết cho 6
d) Chia cho 6 dư 5
e) Chia cho 9 dư 7
3. Một cây cầu , ở 2 bên cầu đều có thanh lan can . Người ta đếm được tất cả có 200 thanh . Hỏi cây cầu đó dài bao nhiêu mét ? Biết rằng 2 thanh liền nhau cách nhau 2 mét .
4.Một ngôi nhà 5 tầng , mỗi tầng cách nhau 4 mét . Nguwpwif ta làm bậc thang từ tầng này lên tầng kia mỗi bậc cao 2 dm . Hỏi cần bao nhiêu bậc thang để lên đến tầng 5 ?
NHỚ VIẾT CÁCH GIẢI RÕ RÀNG . AI NHANH SẼ ĐƯỢC LIKEEEEEEEEEEEEEEEEEE
bạn đánh máy có mỏi tay ko? nếu mỏi thì tk cho mình
Đúng 0
Bình luận (0)
1. So sánh:
a) (4 ( phần nguyên) 8/33) và ( 3 căn bậc 2 )
b) căn bậc 2 của ( 50 + 2 ) và căn bậc 2 của 50 + căn bậc 2 của 2
c) căn bậc 2 của 225 - (1/căn bậc 2 của 5) - 1 và ( căn bậc 2 của 196 ) - 1/căn bậc 2 của 6
giải giúp mik càng nhanh càng tốt nhé, nếu không thì giải một bài cx dc rồi mik tik cho nhé :D