Cho hình lăng trụ đứng có đáy là một hình vuông cạnh a và chiều cao bằng 4a. Tính diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó.
A. 12 πa 2
B. 18 πa 2
C. 9 πa 2
D. 15 πa 2
Cho hình lăng trụ đứng có đáy là một hình vuông cạnh a và chiều cao bằng 2a. Tính diện tích S của mặt cầu ngoại tiếp lăng trụ đó.
A. 18 πa 2
B. 16 πa 2
C. 16 πa 3
D. 6 πa 2
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, các mặt bên đều là hình vuông. Biết rằng mặt cầu ngoại tiếp lăng trụ ABC.A’B’C’ có diện tích bằng 21ᴨ. Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = 18
B. V = 27 3 4
C. V = 6
D. V = 9 3 4
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, các mặt bên đều là hình vuông. Biết rằng mặt cầu ngoại tiếp lăng trụ ABC.A’B’C’ có diện tích bằng 21 π . Tính thể tích V của khối lăng trụ ABC.A’B’C’
![]()
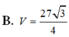
![]()
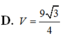
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác vuông tại A, A B = a 3 , BC = 2a, đường thẳng A C ' tạo với mặt phẳng B C C ' B ' một góc 30 ° . Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
A. 6 πa 2
B. 3 πa 2
C. 4 πa 2
D. 24 πa 2
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a 3 , BC=2a. Đường thẳng AC' tạo với mặt phẳng (BCC'B') một góc 30 ° . Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
![]()
![]()
![]()
![]()
a, một lăng trụ đứng có đáy là một tam giác vuông, các cạnh hóc vuông của tam giác vuông là 3cm, 4cm. chiều cao của hình lăng trụ là 9cm.tính thể tích và diện tích xung quanh, diện tích toàn phần của lăng trụ
b, một lăng trụ đứng có đáy là hình chữ nhật có các kích thước là 3cm, 4cm. chiều cao của lăng trụ là 5cm. tính diện tích xung quanh của lăng trụ
a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
a. Thể tích là:
\(\dfrac{3x4}{2}\times9=54cm^3\)
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}5cm\)
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
Một hình lăng trụ đứng ABC.DEF có đáy là một tam giác vuông, chiều cao của lăng trụ là 9 cm. Độ dài 2 cạnh góc vuông của đáy là 3cm và 4 cm (Hình vẽ).
a) Tính độ dài cạnh BC.
b) Tính diện tích xung quanh của hình lăng trụ đứng.
c) Tính diện tích toàn phần của hình lăng trụ đứng.
d) Tính thể tích của hình lăng trụ đứng.
Cho lăng trụ đứng A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi có độ dài cạnh 3cm, góc ∠ A B C = 60 o và chiều cao AA’ của hình lăng trụ bằng 4cm. Tính:
a) Diện tích xung quanh của hình lăng trụ.
b) Thể tích của hình lăng trụ đó.
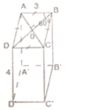
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
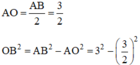
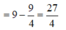
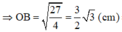
![]()
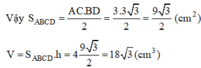
Bình phương cạnh huyền của đáy là: \(6^2+8^2=100\)
\(\Rightarrow\) Cạnh huyền của đáy là \(10\left(cm\right)\)
Diện tích xung quanh lăng trụ là: \(\left(6+8+10\right).3=72\left(cm^2\right)\)
Diện tích đáy lăng trụ là: \(\dfrac{1}{2}.6.8=24\left(cm^2\right)\)
Thể tích lăng trụ là: \(24.3=72\left(cm^3\right)\)