Với giá trị nào của x thì giá trị của mỗi biểu thức sau bằng 0: x x 2 - 4 + 3 x + 2 2

Những câu hỏi liên quan
Với giá trị nào của x thì giá trị của mỗi biểu thức sau bằng 0: 1 x 2 + x + 1 + x - 1
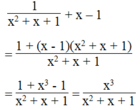
Biểu thức bằng 0 khi x 3 = 0 và x 2 + x + 1 ≠ 0
Ta có: x 3 = 0 ⇒ x = 0;
x 2 + x + 1 = x 2 + 2 . x . 1 / 2 + 1 / 4 + 3 / 4 = x + 1 / 2 2 + 3 / 4 ≠ 0 mọi x.
Vậy với x = 0 thì giá trị của biểu thức bằng 0.
Đúng 0
Bình luận (0)
Với giá trị nào của x thì giá trị của mỗi biểu thức sau bằng 0 :
a) \(\dfrac{x}{x^2-4}+\dfrac{3}{\left(x+2\right)^2}\)
b) \(\dfrac{1}{x^2+x+1}+x-1\)
Q: Với giá trị nào của x thì giá trị của mỗi phân thức sau bằng 0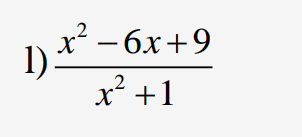
Giá trị phân thức (x^2 - 6x + 9)/(x^2 + 1) bằng 0 khi x^2 - 6x + 9 = 0 <=> (x - 3)^2 = 0
<=> x= 3
Đúng 1
Bình luận (0)
với giá trị nào của x thì biểu thức sau có gt bằng 0
x/(x^2-4)+3/(x+2)^2
Với giá trị nào của x biểu thức sau có giá trị bằng 0
3(2x-3)(3x+2)-2(x+4)(4x-3)+9x(4-x)-6
Cho biểu thức: A = \(\dfrac{x+2}{2x-4}+\dfrac{x-2}{2x+4}+\dfrac{8}{x^2-4}\)
a) Với giá trị nào của x thì biểu thức được xác định.
b) Rút gọn biểu thức A.
c) Tìm giá trị của x để biểu thức A có giá trị bằng -3.
\(a,ĐK:x\ne\pm2\\ b,A=\dfrac{x^2+4x+4+x^2-4x+4+16}{2\left(x-2\right)\left(x+2\right)}\\ A=\dfrac{2x^2+32}{2\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+16}{x^2-4}\\ c,A=-3\Leftrightarrow-3x^2+12=x^2+16\\ \Leftrightarrow4x^2=-4\Leftrightarrow x\in\varnothing\)
Đúng 1
Bình luận (0)
Cho phân thức : x ^ 2 +4 X+4 phần x +2
a) Với điều kiện nào của x thì giá trị của phân thức được xác định
b) Rút gọn phân thức
c) Tìm giá trị của x để giá trị của phân thức bằng 1
d) Có giá trị của x để giá trị của phân thức bằng 0 hay không
1. với giá trị nào của x thì đa thức dư trong mỗi phép chia sau có giá trị bằng 0
a) (2x^4-3x^3+4x^2+1) : (x^2-1)
b) (x^5+2x^4+3x^4+x-3) : (x^2+1)
Với những giá trị nào của x thì giá trị của biểu thức (x + 1)2 - 4 không lớn hơn giá trị của biểu thức (x - 3)2?
A. x < 3/2
B. x > 3/2
C. x ≤ 3/2
D. x ≥ 3/2
Từ giả thiết suy ra (x + 1)2 - 4 ≤ (x - 3)2
Û x2 + 2x + 1 - 4 ≤ x2 - 6x + 9
Û x2 + 2x + 1 - 4 - x2 + 6x - 9 ≤ 0
Û 8x ≤ 12
Û x ≤ 3/2
Vậy x ≤ 3/2là giá trị cần tìm.
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)

















