Cho hai phân thức P Q v à R S
Chứng minh rằng :
Nếu P Q = R S và P ≠ S thì P Q - P = R S - R
2, cho hai phân thức P/Q và R/S . chứng tỏ rằng:
a) nếuP/Q =R/S thì P+Q/Q =R+S/s
b) nếu P/Q =R/S vàP≠Q thìR≠S vàP/Q−P =R/S−R
a: \(\dfrac{P}{Q}=\dfrac{R}{S}\)
nên \(\dfrac{P}{Q}+1=\dfrac{R}{S}+1\)
hay \(\dfrac{P+Q}{Q}=\dfrac{R+S}{S}\)
b: P/Q=R/S=k
=>P=Qk; R=Sk
\(\dfrac{P}{Q-P}=\dfrac{Qk}{Q-Q\cdot k}=\dfrac{k}{1-k}\)
\(\dfrac{R}{S-R}=\dfrac{S\cdot k}{S-S\cdot k}=\dfrac{k}{1-k}\)
Do đó: \(\dfrac{P}{Q-P}=\dfrac{R}{S-R}\)
Cho hai phân thức \(\dfrac{P}{Q}\) và \(\dfrac{R}{S}\).
Chứng tỏ rằng :
a) Nếu \(\dfrac{P}{Q}=\dfrac{R}{S}\) thì \(\dfrac{P+Q}{Q}=\dfrac{R+S}{S}\)
b) Nếu \(\dfrac{P}{Q}=\dfrac{R}{S}\) và \(P\ne Q\) thì \(R\ne S\) và \(\dfrac{P}{Q-P}=\dfrac{R}{S-R}\)
a)
\(\dfrac{P}{Q}=\dfrac{R}{S}\Rightarrow PS=QR\)
\(\Leftrightarrow PS+QS=QR+QS\)
\(\Leftrightarrow S\left(P+Q\right)=Q\left(R+S\right)\)
điều kiện Q,s khác 0 => chia hau vế cho QS
\(\Leftrightarrow\dfrac{S\left(P+Q\right)}{QS}=\dfrac{Q\left(R+S\right)}{QS}\Leftrightarrow\dfrac{\left(P+Q\right)}{Q}=\dfrac{\left(R+S\right)}{S}\) đpcm
Cho hai phân thức P Q và R S thỏa mãn P Q = R S và P ≠ Q.
Chứng minh: R ≠ S và P Q + P = R S + R .
Xuất phát từ điều cần chứng minh Û P(S + R) = R(Q + P)
Rút gọn còn PS = RQ hay P Q = R S (đúng với giả thiết).
1.trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thõa mãn đẳng thức:
a) \(\dfrac{\left(x+2\right)P}{x-2}=\dfrac{\left(x-1\right)Q}{x^2-4}\)
b) \(\dfrac{\left(x+2\right)P}{x^2-1}=\dfrac{\left(x-2\right)Q}{x^2-2x+1}\)
2. cho hai phân thức\(\dfrac{P}{Q}\)và \(\dfrac{R}{S}\). chứng tỏ rằng:
a) nếu \(\dfrac{P}{Q}=\dfrac{R}{S}\)thì \(\dfrac{P+Q}{Q}=\dfrac{R+S}{S}\)
b) nếu \(\dfrac{P}{Q}=\dfrac{R}{S}\) và \(P\ne Q\)thì \(R\ne S\) và \(\dfrac{P}{Q-P}=\dfrac{R}{S-R}\)
Bài 1.
a) Do hai phân thức bằng nhau , ta có :
( x +2)P( x2 - 22) = ( x - 1)Q( x -2)
=( x + 2)P( x - 2)( x + 2) = ( x - 1)Q( x - 2)
Suy ra : P = x - 1 ; Q = ( x + 2)2
b) Do hai phân thức bằng nhau , ta có :
( x + 2)P(x2 - 2x + 1) = ( x - 2)Q( x2 - 1)
= ( x + 2)P( x - 1)2 = ( x - 2)Q( x - 1)( x + 1)
Suy ra : P = ( x - 2)( x + 1) = x2 - x - 2
Q = ( x + 2)( x - 1) = x2 + x + 2
Bài 2. a) Do : \(\dfrac{P}{Q}=\dfrac{R}{S}=>PS=QR\)
Xét : ( P + Q)S= PS + QS = QR + QS = Q( R + S)
-> \(\dfrac{P+Q}{Q}=\dfrac{R+S}{S}\)
b) Do : \(\dfrac{P}{Q}=\dfrac{R}{S}=>PS=QR\)
Xét : ( S - R)P = PS - PR = QR - PR = R( Q - P)
-> \(\dfrac{R-S}{R}=\dfrac{Q-P}{P}\)
- > \(\dfrac{R}{R-S}=\dfrac{P}{Q-P}\)
1. trong mỗi trường hợp sau tìm hai đa thức P và Q thõa mãn đẳng thức
a)\(\frac{\left(x+2\right)P}{x-2}=\frac{\left(x-1\right)Q}{x^2-4}\)
b)\(\frac{\left(x+2\right)P}{x^2-1}=\frac{\left(x-2\right)Q}{x^2-2x+1}\)
2, cho hai phân thức \(\frac{P}{Q}\)và \(\frac{R}{S}\). chứng tỏ rằng:
a) nếu\(\frac{P}{Q}=\frac{R}{S}\) thì \(\frac{P+Q}{Q}=\frac{R+S}{S}\)
b) nếu\(\frac{P}{Q}=\frac{R}{S}\) và\(P\ne Q\) thì\(R\ne S\) và\(\frac{P}{Q-P}=\frac{R}{S-R}\)
Cho hai phân thức \(\frac{P}{Q}\)và \(\frac{R}{S}\). Chứng tỏ rằng :
a) Nếu \(\frac{P}{Q}=\frac{R}{S}\)thì \(\frac{P+Q}{Q}=\frac{R+S}{S};\)
b) Nếu \(\frac{P}{Q}=\frac{R}{S}\)và \(P\ne Q\)thì \(R\ne S\)và \(\frac{P}{Q-P}=\frac{R}{S-R}.\)
Cô ơi, cô đừng giải nhe cô, mà cô hướng dẫn giúp em phương pháp chi tiết, dể hiểu và sử dụng các tính chất, công thức nào để giải từng câu a) và câu b) nhe cô, em cám ơn cô nhiều ạ ? ^^
Bài này lớp 7 thôi mà !
a) Cộng 1 vào 2 vế
b) Nghịch đảo 2 vế,trừ 1 ở 2 vế rồi lại nghịch đảo 2 vế
Cho hai phân thức \(\frac{P}{Q}\)và \(\frac{R}{S}.\)Chứng tõ rằng :
Nếu \(\frac{P}{Q}=\frac{R}{S}\)và \(P\ne Q\)và \(R\ne S\)thì \(\frac{P}{Q-P}=\frac{R}{S-R}.\)
Cô ơi, người ta cho mình 2 điều kiện là : \(P\ne Q,R\ne S.\)để làm gì vậy cô ? Cô ơi, cô giải thích chi tiết và ví dụ vào bài này luôn giúp em nhe cô. Em cám ơn cô ạ. ^^
ta có P/Q = R/S => PS= RQ (1)
P/Q-P = R/S-R => P( S-R) = R(Q-P)
=> PS -PR = RQ-RP
từ (1) => P/Q-P= R/S-R (bn tự kết luận nhé
còn người ta cho Q khác P để Q-P khác 0 vì Q-P là mẫu số và R-S cũng vậy nên S khác R
Cho hai phân thức P Q v à R S
Chứng minh rằng :
Nếu P Q = R S thì P + Q Q = R + S S
Nếu 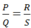 ⇒ PS = QR (1). Vì
⇒ PS = QR (1). Vì 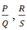 là phân thức
là phân thức
⇒ Q, S khác không. Cộng vào hai vế của đẳng thức (1) với QS
PS + QS = QR + QS ⇒ (P + Q).S = Q.(R + S)
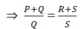
cho hai phân thức\(\frac{P}{Q}\) và  \(\frac{R}{S}\) chứng tỏ rằng
câu(a) \(\frac{P}{Q}\)=\(\frac{R}{S}\)thì \(\frac{P+Q}{Q}\)=\(\frac{R+S}{S}\)
câu(b) \(\frac{P}{Q}\)=\(\frac{R}{S}\)thì P khác S và R khác S và\(\frac{P}{P-Q}\)=\(\frac{R}{S-R}\)
CHỨNG MINH HỘ MÌNH NHÉ MÌNH LIKE CHO
mình chỉ học lop5 thôi thông cảm