Chứng minh rằng đối với tứ giác ABCD bất kỳ ta luôn có:
Những câu hỏi liên quan
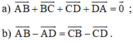
Chứng minh rằng đối với tứ giác ABCD bất kì ta luôn có :
a) \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{O}\)
b) \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\)
Cho 5 điểm bất kỳ. Chứng minh rằng luôn tồn tại 4 điểm tạo thành 1 hình tứ giác lồi.
mik ko bít
I don't now
................................
.............
Đúng 0
Bình luận (0)
cho tứ giác abcd gọi m n p q lần lượt là trung điểm của ab bc cd da gọi e là điểm bất kỳ nằm ngoài tứ giác,f là điểm đối xứng vs e qua m g là điểm đối xứng vs f qua q ,h là điểm đối xứng vs g qua p chứng minh rằng e là điểm đối xứng vs h qua n
bạn ơi giờ bạn có đáp án chưa cho mình xin ké ạ
Đúng 0
Bình luận (0)
cho tứ giác ABCD có AB=AD,BC=CD. Chứng minh rằng ;
a)B và D đối xứng với nhau qua AC
b)Tứ giác ABCD là hình có trục đối xứng
giúp mình với mình cần gấp
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
ta có: BC=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra BD là đường trung trực của AC
hay A và C đối xứng nhau qua BD
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có góc A 70 độ, góc D 80 độ và góc ngoài ở đỉnh C 60 độ.
a Tính góc B của tứ giác ABCD
b Chứng minh rằng tổng 2 đường chéo luôn lớn hơn tổng 2 cạnh đối của tứ giác đó.
Chứng minh rằng trong một tứ giác bất kỳ có ít nhất một góc không nhọn
Tứ giác ABCD.
Giả sử các góc của tứ giác trên đều nhọn .
Khi đó: \(\widehat{A}< 90^o;\widehat{B}< 90^o;\widehat{C}< 90^o;\widehat{D}< 90^o\)
\(\Leftrightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}< 4\times90^o=360^o\)
Mà tổng các góc trong một tam giác luôn bằng 360 độ
=> Vô Lí
=> Trong một tứ giác bất kì có ít nhất một góc không nhọn.
Cho tứ giác ABCD có góc A 70 độ, góc D 80 độ và góc ngoài ở đỉnh C 60 độ.
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng 2 đường chéo luôn lớn hơn tổng 2 cạnh đối của tứ giác đó.
Cho tứ giác ABCD có góc A 70 độ, góc D 80 độ và góc ngoài ở đỉnh C 60 độ.
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng 2 đường chéo luôn lớn hơn tổng 2 cạnh đối của tứ giác đó.
Mọi người giúp mình nhé!
Bài 6. Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo
BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt
vuông góc với AB và AD. Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật.
b) AF song song với BD và KH song song với AC.
999999999999999999999999999999999999
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
H1^ là H mũ 1 à bạn?
Xem thêm câu trả lời