Cho 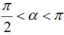 . Xác định dấu của biểu thức
. Xác định dấu của biểu thức 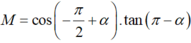
A. M ≥ 0
B. M > 0
C. M ≤ 0
D. M < 0
Cho phương trình: x²-2(m-3)x+(m-4)=0 (1) a) giải phương trình với m=1 b) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt c) Xác định m để phương trình có hai nghiệm trái dấu d)Tính theo m giá trị của biểu thức A=1/x1+1/x2.Tìm m để A € Z để A € Z
a: Khi m=1 thì pt sẽ là: x^2+4x-3=0
=>x=-2+căn 7 hoặc x=-2-căn 7
b: Δ=(2m-6)^2-4(m-4)
=4m^2-24m+36-4m+16
=4m^2-28m+52=(2m-7)^2+3>0
=>PT luôn có hai nghiệm pb
c: PT có hai nghiệm trái dấu
=>m-4<0
=>m<4
Tìm các giá trị của tham số m để biểu thức f(x) = (m-1)x2 + mx +1 đổi dấu hai lần
A: m ≠ 1
B: m ≠ 1 và m ≠ 2
C: m ≠ 2
D: m ∈ R
2: Cho tam thức bậc hai f(x) = x2 - 5x + 6 và a là số thực lớn hơn 3. Tìm khẳng định đúng trong các khẳng định sau.
A: f(a) = 0
B: f(a) > 0
C: f(a) < 0
D: f(a) ≥ 0
2: Cho tam thức bậc hai f(x) = x2 - 4x + 3 và a là số thực nhỏ hơn 1. Tìm khẳng định đúng trong các khẳng định sau.
A: f(a) = 0
B: f(a) > 0
C: f(a) < 0
D: f(a) ≥ 0
Cho M = (−2023). a
2
. b. Biết M là một số nguyên âm. Phát biểu nào sau đây là phát biểu
đúng?
A. b là số nguyên dương B. b là một số nguyên âm
C. b không xác định được dấu D. b = 0
Xác định giá trị của tham số m để phương trình
1 3 x 3 - 1 2 mx 2 - 5 = 0
có nghiệm duy nhất
A. m < - 30 3 B. 0 < m < 1
C. m < 0 D. m > - 30 3
Đáp án: D.
Xét hàm số
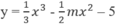
Ta có: y' = x 2 - mx = 0 ⇔ x = 0 hoặc x = 3
Nếu m = 0: Phương trình thành x 3 /3 - 5 = 0, có nghiệm duy nhất.
Nếu m ≠ 0: Phương trình đã cho có nghiệm duy nhất khi và chỉ khi cực đại và cực tiểu của hàm số
![]()
cùng dấu.
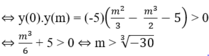
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 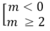
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
∆ ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 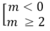
Xác định giá trị của tham số m để hàm số y = x 3 + m x 2 - 3 có cực đại và cực tiểu.
A. m = 3; B. m > 0;
C. m ≠ 0; D. m < 0.
Đáp án: C.
Để có cực đại, cực tiểu, phương trình y' = 3 x 2 + 2mx = 0 phải có hai nghiệm phân biệt.
Phương trình y' = x(3x + 2m) = 0 có hai nghiệm phân biệt x1 = 0, x2 = -2m/3 khi và chỉ khi x ≠ 0.
Xác định giá trị của tham số m để hàm số y = x 3 + m x 2 - 3 có cực đại và cực tiểu.
A. m = 3; B. m > 0;
C. m ≠ 0; D. m < 0.
Đáp án: C.
Để có cực đại, cực tiểu, phương trình y' = 3 x 2 + 2mx = 0 phải có hai nghiệm phân biệt.
Phương trình y' = x(3x + 2m) = 0 có hai nghiệm phân biệt x 1 = 0, x 2 = -2m/3 khi và chỉ khi x ≠ 0.
Cho M = {-1/2} * 7/15 * x {-11/15} * {-30} với x thuộc Q. Hãy xác định dấu của x khi :
a , M < 0
b , M = 0
c , M > 0