Cho hàm số y = 3 x + m - 1 x + 2 Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm A(0 ;1) khi m bằng
A. 1
B. 0
C.m=3
D. m=-3
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Đáp án D
Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
Đồ thị hàm số y = x + x 2 + x + 1 x có 1 tiệm cận đứng là x = 0
Mặt khác lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0 nên đồ thị hàm số có 2 tiệm cận ngang
Xét hàm số y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2 suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng
tìm m thỏa mãn yêu cầu bài toán
a) đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) có đường tiệm cận đứng đi qua điểm M (3;-1)
b) đường thẳng x = -2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
c) biết đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\) có tiệm cận đứng là x = 2 và tiệm cận ngang y = 3. Tính 2a+3b
d) đồ thị hàm số \(y=\dfrac{x+2}{x^2+2x+m^2-3m}\) có 2 đường tiệm cận đứng
a: \(\lim\limits_{x\rightarrow-\dfrac{3m}{2}}\dfrac{x+3}{2x+3m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\dfrac{3m}{2}}2x+3m=0\\\lim\limits_{x\rightarrow-\dfrac{3m}{2}}x+3=\dfrac{-3m}{2}+3\end{matrix}\right.\)
=>x=-3m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\)
Để tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) đi qua M(3;-1) thì \(-\dfrac{3m}{2}=3\)
=>-1,5m=3
=>m=-2
b: \(\lim\limits_{x\rightarrow-m}\dfrac{2x-3}{x+m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-m}2x-3=-2m-3\\\lim\limits_{x\rightarrow-m}x+m=0\end{matrix}\right.\)
=>x=-m là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
Để x=-2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\) thì -m=-2
=>m=2
c: \(\lim\limits_{x\rightarrow\dfrac{2}{b}}\dfrac{ax+1}{bx-2}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow\dfrac{2}{b}}ax+1=a\cdot\dfrac{2}{b}+1\\\lim\limits_{x\rightarrow\dfrac{2}{b}}bx-2=b\cdot\dfrac{2}{b}-2=0\end{matrix}\right.\)
=>Đường thẳng \(x=\dfrac{2}{b}\) là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\)
=>2/b=2
=>b=1
=>\(y=\dfrac{ax+1}{x-2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow+\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
=>Đường thẳng y=a là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{ax+1}{x-2}\)
=>a=3
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\) có đường tiệm cận ngang đi qua điểm A (-1;3)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = -2
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m+3\right)x-5}{x+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m+3\right)x-5}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
=>Đường thẳng y=2m+3 là đường tiệm cận ngang duy nhất của đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\)
Để đường thẳng y=2m+3 đi qua A(-1;3) thì 2m+3=3
=>2m=0
=>m=0
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
=>Đường thẳng \(y=m^2-3m\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
=>\(m^2-3m=-2\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>m=1 hoặc m=2
Cho các mệnh đề sau
(1) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → x 0 f x = y 0 h o ặ c lim x → x 0 f x = y 0
(2) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → - ∞ f x = y 0 h o ặ c lim x → + ∞ f x = y 0
(3) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = + ∞ h o ặ c lim x → x 0 - f x = - ∞
(4) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = - ∞ h o ặ c lim x → x 0 - f x = - ∞
Trong các mệnh đề trên, số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. 4
Chọn C
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D = ℝ \ 3
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. (1), (3), (4)
B. (3), (4)
C. (2), (3), (4)
D. (1), (4)
Đáp án B
Sai lầm thường gặp: Tập xác định D = ℝ \ 3 .
Đạo hàm y ' = − 2 x − 3 2 ,0, ∀ x ∈ D ⇒ Hàm số nghịch biến trên ℝ \ 3 , hoặc làm số nghịch biến trên − ∞ ; 3 ∪ 3 ; + ∞ . Hàm số không có cực trị.
Tiệm cận đứng: x=3; tiệm cận ngang: y=1. Đồ thị hàm số nhận giao điểm I 3 ; 1 của hai đường tiệm cận làm tâm đối xứng.
Từ đó nhiều học sinh kết luận các mệnh đề 1 , 3 , 4 đúng và chọn ngay A.
Tuy nhiên đây là phương án sai.
Phân tích sai lầm:
Mệnh đề (1) sai, sửa lại: hàm số nghịch biến trên mỗi khoảng − ∞ ; 3 và 3 ; + ∞ . Học sinh cần nhớ rằng, ta chỉ học định nghĩa hàm số đồng biến (nghịch biến) trên khoảng, đoạn, nửa khoảng; chứ không có trên những khoảng hợp nhau.
Mệnh đề (2) sai. Đồ thị hàm số có một tiệm cận đứng là x=3, một tiệm cận ngang là y=1.
Mệnh đề 3 , 4 đúng.
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D=R\{3}.
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị.
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. 1,2,3.
B. 3,4.
C. 2,3,4.
D. 1,4.
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\) có đường tiệm cận ngang đi qua điểm M (-2;1)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = 1
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-5-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
=>Đường thẳng \(y=\dfrac{m-5}{2}\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\)
Để đường tiệm cận ngang \(y=\dfrac{m-5}{2}\) đi qua M(-2;1) thì \(\dfrac{m-5}{2}=1\)
=>m-5=2
=>m=7
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
=>\(y=2m-1\) là đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
=>2m-1=1
=>2m=2
=>m=1
tìm m thỏa mãn yêu cầu bài toán
a) đồ thị hàm số \(y=\dfrac{mx-1}{2x+m}\) có đường tiệm cận đứng đi qua điểm A (-1;\(\sqrt{2}\))
b) đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
c) biết đồ thị hàm số \(y=\dfrac{\left(m+1\right)x+2}{x-n+1}\) nhận trục hoành và trục tung làm 2 đường tiệm cận. Tính m+n
d) đồ thị hàm số \(y=\dfrac{x-1}{x^2+2\left(m-1\right)x+m^2-2}\) có 2 đường tiệm cận đứng
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{mx-1}{2x+m}=\lim\limits_{x\rightarrow+\infty}\dfrac{m-\dfrac{1}{x}}{2+\dfrac{m}{x}}=\dfrac{m}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{mx-1}{2x+m}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-\dfrac{1}{x}}{2+\dfrac{m}{x}}=\dfrac{m}{2}\)
Vậy: x=m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{mx-1}{2x+m}\)
Để x=m/2 đi qua \(A\left(-1;\sqrt{2}\right)\) thì \(\dfrac{m}{2}=-1\)
=>\(m=-1\cdot2=-2\)
b: \(\lim\limits_{x\rightarrow-\infty}\dfrac{x-2}{2x-m}=\lim\limits_{x\rightarrow-\infty}\dfrac{1-\dfrac{2}{x}}{2-\dfrac{m}{x}}=\dfrac{1}{2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x-2}{2x-m}=\lim\limits_{x\rightarrow+\infty}\dfrac{1-\dfrac{2}{x}}{2-\dfrac{m}{x}}=\dfrac{1}{2}\)
=>x=1/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
=>Không có giá trị nào của m để đường thẳng x=1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
Mọi người ơi cho mình hỏi bài này với ạ
1.Số đường tiệm cận của hàm số y=\(\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}\) là
2.Tìm tất cả các tiệm cận đứng của đồ thị hàm số y=\(\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}\)
Mình cảm ơn mọi người nhiều lắm !!!!!
1.
Điều kiện xác định của căn thức: \(\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{1-1}{1}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{-1-1}{-1}=2\Rightarrow y=2\) là 1 TCN
\(\lim\limits_{x\rightarrow-5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}+5}{0}=+\infty\Rightarrow x=-5\) là 1 TCĐ
\(\lim\limits_{x\rightarrow5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}-5}{0}=+\infty\Rightarrow x=5\) là 1 TCĐ
Hàm có 4 tiệm cận
2.
Căn thức của hàm luôn xác định
Ta có:
\(\lim\limits_{x\rightarrow2}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\lim\limits_{x\rightarrow2}\dfrac{\left(2x-1\right)^2-\left(x^2+x+3\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(3x+1\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{3x+1}{\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}=\dfrac{-7}{6}\) hữu hạn
\(\Rightarrow x=2\) ko phải TCĐ
\(\lim\limits_{x\rightarrow3}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\dfrac{5-\sqrt{15}}{0}=+\infty\)
\(\Rightarrow x=3\) là tiệm cận đứng duy nhất
Cho hàm số y=f(x) xác định, liên tục trên tập R\{1} và có bảng biến thiên
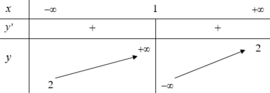
Số mệnh đề đúng trong các mệnh đề sau là?
1. Đường thẳng y=2 là đường tiệm cận ngang của đồ thị hàm số.
2. Đường thẳng x=1 là đường tiệm cận đứng của đồ thị hàm số.
3. Hàm số đồng biến trên các khoảng - ∞ ; 1 và 1 ; + ∞
A. 0.
B. 1
C. 2.
D. 3