1. Tìm tất cả các giá trị thực của tham số m để hàm số y= mx - sin3x đồng biến trên khoảng ( trừ vô cùng ; cộng vô cùng) 2. Tìm tất cả các giá trị thực của tham số m để hàm số y = x + mcosx đồng biến trên khoảng( trừ vô cùng ; cộng vô cùng)
1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)
Tìm tất cả các giá trị thực của tham số m để hàm số y = sin 3 x - 3 cos 2 x - m sin x - 1 đồng biến trên đoạn [0; π 2 ].
A. 
.
B. 
.
C. 
.
D. 
.
Chọn B.
Đặt 
Xét hàm số 
Ta có 
Để hàm số 
đồng biến trên 
cần:
Xét hàm số 
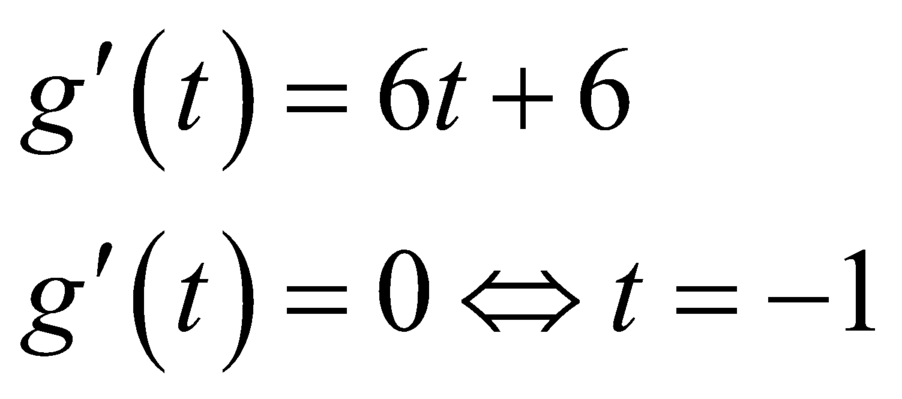
Bảng biến thiên
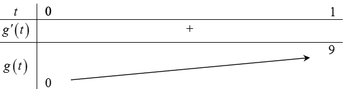
Nhìn vào bảng biến thiên ta thấy với 
thì hàm số 
đồng biến trên 
, hàm số 
đồng biến trên đoạn 
.
Tìm tất cả các giá trị thực của tham số m để hàm số y = sin 3 x - 3 cos 2 x - m sin x - 1 đồng biến trên đoạn 0 ; π 2
A. m > -3
B. m ≤ 0
C. m ≤ - 3
D. m > 0
Đáp án B
Đặt t = sin x ⇒ t ' = c o s x ≥ 0 ; ∀ c ∈ 0 ; π 2 suy ra 0 ≤ t ≤ 1
Khi đó bài toán trở thành :Tìm m để hàm số f t = t 3 + 3 t 2 - m t - 4 đồng biến trên [0;1]
Ta có f ' t = 3 t 2 + 6 t - m ≥ 0 ⇔ m ≤ 3 t 2 + 6 t ; ∀ t ∈ 0 ; 1 ⇔ m ≤ m i n 0 ; 1 g t = 3 t 2 + 6 t
Xét hàm số trên , suy ra m i n 0 ; 1 g t = g 0 = 0 . Vậy m ≤ 0
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = m cos x + 1 cos x + m đồng biến trên khoảng 0 ; π 3
A. - 1 ; 1
B. - ∞ ; - 1 ∪ 1 ; + ∞
C. [ - 1 ; - 1 2 )
D. - 1 ; - 1 2
Tìm tất cả các giá trị thực của m để hàm số y = cos x − 1 cos x − m đồng biến trên 0 ; π 2 .
A. m ≥ 1.
B. m > 1.
C. − 1 ≤ m ≤ 1.
D. m < 1.
Đáp án B
Đặt ẩn phụ, tìm điều kiện của ẩn phụ, xét hàm.
Khi m=1 ta có: y=1 là hàm hằng nên m=1 không thỏa mãn.
Khi m ≠ 1 . Đặt t = cos x . Vì x ∈ 0 ; π 2 nên t ∈ 0 ; 1
Xét hàm y = t − 1 t − m có y ' = t − m − t + 1 t − m 2 = 1 − m t − m 2 . .
Để hàm số đã cho đồng biến trên 0 ; π 2 thì hàm số y = t − 1 t − m nghịch biến trên 0 ; 1
⇔ 1 − m < 0 1 < 1 − m 1 − m < 0 ⇔ m > 1 m < 0 m > 1 ⇔ m > 1.
Tìm các giá trị thực của m để đồ thị hàm số y = 1 3 x 3 − 2 mx 2 + x + m − 1 đồng biến trên R.
A. m ≤ 1 4
B. m ≥ 1 2
C. m ∈ ℝ
D. m ≤ 1 2
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 2 m x 2 + m đồng biến trên khoảng ( - ∞ ; 0 )
A.
B. 
C. Không có m
D. Mọi 
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 2 m x 2 + m đồng biến trên khoảng - ∞ ; 0
A. m ≥ 0
B. m ≤ 0
C. Không có m
D. Mọi m ∈ R
bài1cho hàm số Y=(2-m)x-2tìm các giá trị của m để HS bậc nhất.tìm hệ số a,b
bài 2, cho hàm số Y=(m-5)x+1.tìm các giá trị để hàm số
a, đồng biến trên R b,nghịch biến trên R
bài 3,cho 2 HS bậc nhất Y=(3-m)\(\times\)x+2(d1) và Y=2x+m(d2)
a,tìm giá trị của m để đồ thị hai hàm số song song với nhau
b,tìm giá trị của m để đồ thị hai hàm số cắt nhau
c,tìm giá trị của m để đồ thị hai hàm số cắt nhau tại 1 điểm trên trục tung
bài 4, cho HS Y=2x=1.tìm hệ số góc ,tung độ gốc,vẽ đồ thị HS trên ,tính góc tạo bởi đường thẳng trên với trục ox
Bài 1:
Để hàm số y=(2-m)x-2 là hàm số bậc nhất thì 2-m<>0
=>m<>2
a=2-m
b=-2
Bài 2:
a: Để hàm số y=(m-5)x+1 đồng biến trên R thì m-5>0
=>m>5
b: Để hàm số y=(m-5)x+1 nghịch biến trên R thì m-5<0
=>m<5
Bài 3:
a: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}3-m=2\\2\ne m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=1\)
b: Để (d1) cắt (d2) thì \(3-m\ne2\)
=>\(m\ne1\)
c: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}3-m\ne2\\m=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m=2\end{matrix}\right.\)
=>m=2
