Trong mặt phẳng tọa độ , cho tam giác MNP có M(1;-1) : N(5; -3) và P thuộc trục Oy, trọng tâm G của tam giác nằm trên trục Ox.Toạ độ của điểm P là
A.(0;4)
B.(4;0)
C.(2;4)
D.(2;0)
Những câu hỏi liên quan
Trong mặt phẳng Oxy cho tam giác MNP với
M
1
;
-
1
,
N
3
;
1
,
P
5
;
-
5
;. Tọa độ tâm I đường tròn ngoại tiếp tam giác MNP là: A.
I
4
;
2
B.
I...
Đọc tiếp
Trong mặt phẳng Oxy cho tam giác MNP với M 1 ; - 1 , N 3 ; 1 , P 5 ; - 5 ;. Tọa độ tâm I đường tròn ngoại tiếp tam giác MNP là:
A. I 4 ; 2
B. I - 4 ; 2
C. I 4 ; - 4
D. I 4 ; - 2
trong mặt phẳng tọa độ oxy biết M(2;3);N(6;2);P(5;0) tìm tọa độ trọng tâm G cửa tam giác MNp
Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có Mleft( {2;1} right),Nleft( { - 1;3} right),Pleft( {4;2} right)a) Tìm tọa độ của các vectơ overrightarrow {OM} ,overrightarrow {MN} ,overrightarrow {MP} b) Tính tích vô hướng overrightarrow {MN} .overrightarrow {MP} c) Tính độ dài các đoạn thẳng MN,MPd) Tính cos widehat {MNP}e) Tìm tọa độ trung điểm I của NP và trọn tâm G của tam giác MNP
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có \(M\left( {2;1} \right),N\left( { - 1;3} \right),P\left( {4;2} \right)\)
a) Tìm tọa độ của các vectơ \(\overrightarrow {OM} ,\overrightarrow {MN} ,\overrightarrow {MP} \)
b) Tính tích vô hướng \(\overrightarrow {MN} .\overrightarrow {MP} \)
c) Tính độ dài các đoạn thẳng \(MN,MP\)
d) Tính \(\cos \widehat {MNP}\)
e) Tìm tọa độ trung điểm I của NP và trọn tâm G của tam giác MNP
a) Ta có: \(\overrightarrow {OM} = \left( {2;1} \right),\overrightarrow {MN} = \left( { - 3;2} \right),\overrightarrow {MP} = \left( {2;1} \right)\)
b) Ta có: \(\overrightarrow {MN} .\overrightarrow {MP} = - 3.2 + 2.1 = - 4\)
c) Ta có: \(MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( { - 3} \right)}^2} + {2^2}} = \sqrt {13} ,MP = \left| {\overrightarrow {MP} } \right| = \sqrt {{2^2} + {1^2}} = \sqrt 5 \)
d) Ta có: \(\cos \widehat {MNP} = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {MP} } \right|}} = \frac{- 4}{{\sqrt {13} .\sqrt 5 }} = \frac{- 4}{{\sqrt {65} }}\)
e) Tọa độ trung điểm I của đoạn NP là: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_N} + {x_P}}}{2} = \frac{3}{2}\\{y_I} = \frac{{{y_N} + {y_P}}}{2} = \frac{5}{2}\end{array} \right. \Leftrightarrow I\left( {\frac{3}{2};\frac{5}{2}} \right)\)
Tọa độ trọng tâm G của tam giác MNP là: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3}\\{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_G} = \frac{5}{3}\\{y_C} = 2\end{array} \right. \Leftrightarrow G\left( {\frac{5}{3};2} \right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, M,N,P là tọa độ điểm biểu diễn của số phức
z
1
-
5
+
6
i
;
z
2
-
4
-
i
;
z
3
4
+...
Đọc tiếp
Trong mặt phẳng Oxy, M,N,P là tọa độ điểm biểu diễn của số phức z 1 = - 5 + 6 i ; z 2 = - 4 - i ; z 3 = 4 + 3 i
Tọa độ trực tâm H của tam giác MNP là:
A. (3;1)
B. (-1;3)
C. (2;-3)
D. (-3;2)
Chọn D.
M(-5;6), N(-4;-1), P(4;3)
Gọi H(x;y) là trực tâm ∆ MNP, ta có:
Đúng 0
Bình luận (0)
Trong mặt phẳng oxy M,N,P là tọa độ điểm biểu diễn của số phức
z
1
-
5
+
6
i
,
z
2
-
4
-
i
;
z
3
4
+
3
i
Tọa độ trực tâm H của tam giác MNP là: A.
3
;
1
B.
-
1...
Đọc tiếp
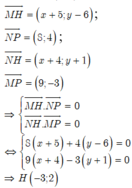
Trong mặt phẳng oxy M,N,P là tọa độ điểm biểu diễn của số phức z 1 = - 5 + 6 i , z 2 = - 4 - i ; z 3 = 4 + 3 i
Tọa độ trực tâm H của tam giác MNP là:
A. 3 ; 1
B. - 1 ; 3
C. 2 ; - 3
D. - 3 ; 2
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N, P là điểm biểu diễn của 3 số phức:
z
1
8
+
i
;
z
2
1
+
4
i
;
z
3
5
+
x
i
.Tìm x để tam giác MNP vuông tại P A. 1 và 2 B. 0 và 7 C. -1 và -7 D. 3 và 5
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N, P là điểm biểu diễn của 3 số phức: z 1 = 8 + i ; z 2 = 1 + 4 i ; z 3 = 5 + x i .Tìm x để tam giác MNP vuông tại P
A. 1 và 2
B. 0 và 7
C. -1 và -7
D. 3 và 5
Ta có 3 điểm M ( 8;3 ), N ( 1;4 ), P ( 5;x ) ⇒ M P → - 3 ; x ; - 3 , N P → 4 ; x ; - 4
∆ M N P vuông tại P ⇔ M P → . N P → = 0 ⇔ - 12 + x - 3 x - 4 = 0 ⇔ x = 0 ; x = 7 .
Đáp án B
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ oxy cho tam giác ABC có A(2;3); B ( -3;1);C (0;-1) .tìm tọa độ các đỉnh cua tam giac MNP sao cho A,B,C lan luot la trung diem cua cac canh MN,NP,PM
Trong mặt phẳng tọa độ Oxy, cho ba điểm M,N,P là điểm biểu diễn của 3 số phức:
z
1
8
+
3
i
;
z
2
1
+
4
i
;
z
3
5...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm M,N,P là điểm biểu diễn của 3 số phức: z 1 = 8 + 3 i ; z 2 = 1 + 4 i ; z 3 = 5 + x i .Với giá trị nào của x thì tam giác MNP vuông tại P?
A. 1 và 2
B. 0 và 7
C. -1 và -7
D. 3 và 5
Chọn B.
Ta có 3 điểm M(8;3), N(1;4), P(5;x)
Để ∆ MNP vuông tại P
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N , P là điểm biểu diễn của 3 số phức:
z
1
8
+
3
i
,
z
2
1
+
4
i
,
z
3
5
+
x
i
.Với giá trị nào của x thì tam giác MNP vuông tại P? A. 1 và 2 B. 0 và 7 C. - 1 và - 7 D. 3 và 5
Đọc tiếp
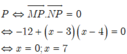
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N , P là điểm biểu diễn của 3 số phức: z 1 = 8 + 3 i , z 2 = 1 + 4 i , z 3 = 5 + x i .Với giá trị nào của x thì tam giác MNP vuông tại P?
A. 1 và 2
B. 0 và 7
C. - 1 và - 7
D. 3 và 5
