Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 8 tấm , tính xác suất để chọn được 5 tấm mang số lẻ, 3 tấm mang số chẵn trong đó ít nhất 2 tấm thẻ mang số chia hết cho 4. Kết quả đúng là:
A. 1008 4199
B. 3695 4199
C. 504 4199
D. 3191 4199
Đáp án C
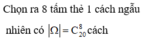
Trong 20 tấm thẻ có 10 tấm mang
số lẻ, có 5 tấm mang số chẵn không chia hết cho 4 và 5 tấm thẻ mang số chẵn
chia hết cho 4
TH1: Lấy được 5 tấm mang số lẻ, 2 tấm mang số chẵn chia hết cho 4 và tấm mang 1 số chẵn không chi hết cho 4 có 
TH2: Lấy được 5 tấm mang số lẻ, 3 tấm mang số chẵn chia hết cho 4 có
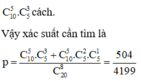
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 8 tấm , tính xác suất để chọn được 5 tấm mang số lẻ, 3 tấm mang số chẵn trong đó ít nhất 2 tấm thẻ mang số chia hết cho 3.
Trong các số từ 1 tới 20, có 3 số lẻ chia hết cho 3 là \(\left\{3;9;15\right\}\), 3 số chẵn chia hết cho 3 là \(\left\{6;12;18\right\}\), có 7 số lẻ ko chia hết cho 3, 7 số chẵn ko chia hết cho 3
Chọn 8 thẻ bất kì: \(C_{20}^8\) cách
Chọn 8 thẻ trong đó ko thẻ nào chia hết cho 3: có \(C_7^5.C_7^3\) cách
Chọn 8 thẻ trong đó có đúng 1 thẻ chia hết cho 3:
TH1: thẻ chia hết cho 3 là thẻ chẵn: \(C_3^1.C_7^2.C_7^5\) cách
TH2: thẻ chia hết cho 3 là thẻ lẻ: \(C_3^1.C_7^4.C_7^3\) cách
Xác suất: \(\dfrac{C_{20}^8-\left(C_7^3.C_7^5+C_3^1.C_7^2.C_7^5+C_3^1.C_7^4.C_7^3\right)}{C_{20}^8}=...\)
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất trong 5 tấm được chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là
A. 75 94
B. 25 646
C. 170 646
D. 175 646
Trong 20 tấm thẻ từ 1 đến 20 có 10 tấm thẻ mang số lẻ, 10 tấm thẻ mang số chẵn trong đó có 5 tấm thẻ chia hết cho 5. Gọi A là biến cố: " chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4"
TH1: Chọn được 3 tấm thẻ mang số lẻ 1 tấm thẻ mang số chẵn chia hết cho 4 và một tấm chẵn mang số không chia hết cho 4 có: 
TH2: Chọn được 3 tấm thẻ mang số lẻ và 2 tấm thẻ mang số chẵn và chia hết cho 4 có:
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất trong 5 tấm được chọn có 3 tấm mang số lẻ, 3 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là
A. 75/94.
B. 125/646.
C. 170/646.
D. 175/646
Có 30 tấm thẻ được đánh số thứ tự từ số 1 đến số 30 mỗi tấm một số. Chọn ngẫu nhiên 10 tấm thẻ. Tính xác suất để chọn được 5 tấm thẻ mang số lẻ, 5 tấm mang số chẵn trong đó có đúng 1 tấm thẻ mang số chia hết cho 10
gọi\(\Omega\) là không gian mẫu để rút ra 10 tấm thẻ trong 30 tấm==>n(\(\Omega\))=C1030 =30045015
gọi A là biến cố "lấy 10 tấm thẻ trong đó có 5 tấm mang số lẻ, 5 tấm chẵn trong đó có 1 tấm chia hết cho 10"
nx: có 30 tấm đánh số từ 1->30 ------->15 tấm lẻ, 15 tấm chẵn, có 3 tấm chứa số 10, 20,30 là chia hết cho 10
- trường hợp rút 5 tấm lẻ là :C515 =3003 cách
- TH rút 5 tấm chẵn trong đó có 1 tấm chia hết cho 10 là
3xC412 =1485 cách
=======> n(A)=1485x3003=4459455 cách====>P(A)=99/667
Có 10 tấm thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để trong 10 tấm thẻ có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn và có đúng một tấm thẻ mang số chia hết cho 10.
Có 10 tấm thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để trong 10 tấm thẻ có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn và có đúng một tấm thẻ mang số chia hết cho 10.
A. 99 667
B. 634 667
C. 33 667
D. 568 667
Có 30 tấm thẻ được đánh số thứ tự từ 1 đến 30. Chọn ngẫu nhiên 10 tấm. Tính xác suất lấy được 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó có đúng một tấm thẻ mang số chia hết cho 10
A. 99 667
B. 568 667
C. 33 667
D. 634 667
Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Xác suát để có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn, trong đó chỉ có đúng 1 tấm thẻ mang số chia hết cho 5 là:
