Thể tích của khối lập phương ABCD.A'B'C'D' có đường chéo AC'= 6 bằng
A. 3 3
B. 2 3
C. 2
D. 2 2
Tính thể tích V của khối lập phương ABCD.A'B'C'D' biết đường chéo AC'=a 3 .
A. a 3 3
B. 3 3 a 3
C. 3 6 a 3 4
D. a 3
Chọn D.
Gọi cạnh hình lập phương là x. Ta có
![]()
Cho hình lập phương ABCD.A'B'C'D' có đường chéo bằng a 3 . Tính thể tích khối chóp A'.ABCD.
A. a 3 3
B. C
C. a 3
D. 2 2 a 3
Đáp án A
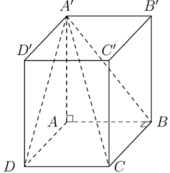
Ta có: hình lập phương ABCD.A'B'C'D' có đường chéo bằng a 3
Suy ra cạnh của hình lập phương bằng a.
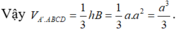 Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3
Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3
Cho hình lập phương A B C D . A ' B ' C ' D ' có đường chéo bằng a 3 . Tính thể tích khối chóp A ' A B C D ?
A. a 3 3
B. 2 a 3 2 3
C. a 3
D. 2 a 3 2
Thể tích của khối lập phương ABCD,A’B’C’D’ có đường chéo AC’ = 6 bằng
A. 3 3
B. 2 3
C. 2
D. 2 2
Cho hình lập phương ABCD.A'B'C'D' có AC = 5cm. Hãy tính:
a) Độ dài cạnh hình lập phương;
b) Độ dài đường chéo hình lập phương;
c) Thể tích hình lập phương.
Khối lập phương ABCD. A’B’C’D’ có đường chéo AC’= 6 cm có thể tích gần bằng.
A. 0.8 lít
B. 0.024lít
C. 0.08lít
D. 0.04lít
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2. Cắt hình lập phương bằng một mặt phẳng chứa đường chéo AC’. Tìm giá trị nhỏ nhất của diện tích thiết diện thu được.
A. 4
B. 4 2
C. 6
D. 2 6
Cho hình lập phương ABCD.A'B'C'D'. Gọi M là điểm trên đường chéo CA' sao cho M C → = - 3 M A ' → . Tính tỉ số giữa thể tích V 1 của khối chóp M.ABCD và thể tích V 2 của khối lập phương.
A. V 1 V 2 = 1 3
B. V 1 V 2 = 3 4
C. V 1 V 2 = 1 9
D. V 1 V 2 = 1 4
Đáp án D
Ta có V 1 = 1 3 . 3 a 4 . a 2 = a 3 4 ; V 2 = a 3 ⇒ V 1 V 2 = 1 4 .
Cho hình lập phương ABCD.A'B'C'D' với O' là tâm hình vuông A'B'C'D'. Biết rằng tứ diện O'BCD có thể tích bằng 6 a 3 . Tính thể tích V của khối lập phương ABCD.A'B'C'D'.
A. V = 12 a 3
B. V = 6 3 a 3
C. V = 2 3 a 3
D. V = 9 3 a 3
Đáp án là B

Gọi x là độ dài của cạnh hình lập phương
Ta có: 

Theo giả thiết, 
![]()
Vậy thể tích lập phương là: ![]()