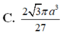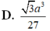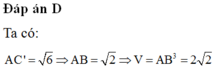Các câu hỏi tương tự
Tính thể tích V của khối lập phương ABCD.ABCD biết đường chéo ACa
3
. A.
a
3
3
B.
3
3
a
3
C.
3
6...
Đọc tiếp
Tính thể tích V của khối lập phương ABCD.A'B'C'D' biết đường chéo AC'=a 3 .
A. a 3 3
B. 3 3 a 3
C. 3 6 a 3 4
D. a 3
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khi đó thể tích hình chóp A.A'BCD' bằng:
A. a 3 /2 B. a 3 /3
C. a 3 /4 D. a 3 /6
Cho hình lập phương ABCD.ABCD có đường chéo bằng
a
3
. Tính thể tích khối chóp A.ABCD. A.
a
3
3
B. C C.
a
3
D.
2
2
a
3
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có đường chéo bằng a 3 . Tính thể tích khối chóp A'.ABCD.
A. a 3 3
B. C
C. a 3
D. 2 2 a 3
Cho hình lập phương ABCD.ABCD có cạnh bằng 2. Cắt hình lập phương bằng một mặt phẳng chứa đường chéo AC’. Tìm giá trị nhỏ nhất của diện tích thiết diện thu được. A. 4 B. 4
2
C.
6
D.
2
6
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2. Cắt hình lập phương bằng một mặt phẳng chứa đường chéo AC’. Tìm giá trị nhỏ nhất của diện tích thiết diện thu được.
A. 4
B. 4 2
C. 6
D. 2 6
Bài 1. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. a. Tính độ dài đường chéo của hình lập phương. b. Tính góc giữa AC' và mặt đáy c. Tính góc giữa AC và B'C' d. Tính khoảng cách từ A đến (A'BD)
Cho hình lập phương ABCD.ABCD với O là tâm hình vuông ABCD. Biết rằng tứ diện OBCD có thể tích bằng 6
a
3
. Tính thể tích V của khối lập phương ABCD.ABCD. A. V 12
a
3
B. V 6
3
a
3
C. V 2
3
a
3
D. V 9
3...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' với O' là tâm hình vuông A'B'C'D'. Biết rằng tứ diện O'BCD có thể tích bằng 6 a 3 . Tính thể tích V của khối lập phương ABCD.A'B'C'D'.
A. V = 12 a 3
B. V = 6 3 a 3
C. V = 2 3 a 3
D. V = 9 3 a 3
Cho hình lập phương ABCD.ABCD có khoảng cách giữa hai đường thẳng AB′ và BD bằng
2
3
a
3
Thể tích của khối lập phương ABCD.A’B’C’D’ bằng A. 8
a
3
B.
a
3
C.
3
3
a
3...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có khoảng cách giữa hai đường thẳng AB′ và BD bằng 2 3 a 3
Thể tích của khối lập phương ABCD.A’B’C’D’ bằng
A. 8 a 3
B. a 3
C. 3 3 a 3
D. 3 6 4 a 3
Cho hình lập phương ABCD.ABCD có diện tích tam giác AC D bằng
a
2
3
. Tính thể tích V của hình lập phương. A.
V
8
a
3
B.
V
a
3
C.
V
2
2
a
3
D.
V
4...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có diện tích tam giác AC
D' bằng a 2 3 . Tính thể tích V của hình lập phương.
A. V = 8 a 3
B. V = a 3
C. V = 2 2 a 3
D. V = 4 2 a 3
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Khối nón đỉnh A, đáy là đường tròn đi qua ba điểm ABD có thể tích bằng
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khối nón đỉnh A, đáy là đường tròn đi qua ba điểm A'BD có thể tích bằng
![]()