Đáp án A
Gọi x là độ dài cạnh của hình lập phương. Có:
A C = A D ' = C D ' = x 2 ⇒ S A C D ' = x 2 3 4 ⇔ x 2 3 4 = a 2 3 ⇔ x = 2 a
Vậy V=x3=(2a)3=8a3
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khi đó thể tích hình chóp A.A'BCD' bằng:
A. a 3 /2 B. a 3 /3
C. a 3 /4 D. a 3 /6
Tính thể tích V của khối lập phương ABCD.ABCD biết đường chéo ACa
3
. A.
a
3
3
B.
3
3
a
3
C.
3
6...
Đọc tiếp
Tính thể tích V của khối lập phương ABCD.A'B'C'D' biết đường chéo AC'=a 3 .
A. a 3 3
B. 3 3 a 3
C. 3 6 a 3 4
D. a 3
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính thể tích V của khối tứ diện AB'C'D'.
Cho hình lập phương ABCD.ABCD với O là tâm hình vuông ABCD. Biết rằng tứ diện OBCD có thể tích bằng 6
a
3
. Tính thể tích V của khối lập phương ABCD.ABCD. A. V 12
a
3
B. V 6
3
a
3
C. V 2
3
a
3
D. V 9
3...
Đọc tiếp
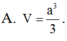
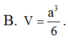
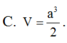
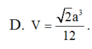
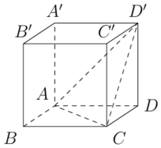
Cho hình lập phương ABCD.A'B'C'D' với O' là tâm hình vuông A'B'C'D'. Biết rằng tứ diện O'BCD có thể tích bằng 6 a 3 . Tính thể tích V của khối lập phương ABCD.A'B'C'D'.
A. V = 12 a 3
B. V = 6 3 a 3
C. V = 2 3 a 3
D. V = 9 3 a 3
20 tháng 7 2021 lúc 21:15
Cho hình chóp tam giác đều S.ABCD, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 60. Tính thể tích V của hình chóp S.ABCD. A)a³✓3/2 B)a³✓3/6 C)a³✓3/12 D)a³✓3/24
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3 B. V/9
C. V/27 D. V/81.
Cho hình lập phương ABCD.ABCD. Gọi (H) là hình trụ tròn xoay ngoại tiếp hình lập phương đó. Khi đó:
V
H
V
ABCD
.
A
B
C
D...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình trụ tròn xoay ngoại tiếp hình lập phương đó. Khi đó: V H V ABCD . A ' B ' C ' D '
A. 3/2 B. π /2
C. π /3 D. π /( 3 )
Cho hình lập phương ABCD.ABCD, biết diện tích DBDC bằng
a
2
3
. Tính thể tích hình lập phương đó theo a. A. V
2
a
3
2
B. V
a
3
C. V 8
a
3
D. V 3
a
3
3
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D', biết diện tích DB'D'C bằng a 2 3 . Tính thể tích hình lập phương đó theo a.
A. V = 2 a 3 2
B. V = a 3
C. V = 8 a 3
D. V = 3 a 3 3