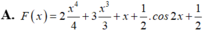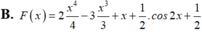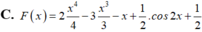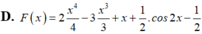Cho F(x) là nguyên hàm của hàm số f(x) = sin2x và F ( π 4 ) = 1 Tính F π 6
A. 1/2
B. 0
C. 5/4
D. 3/4
Những câu hỏi liên quan
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
1
1
+
sin
2
x
với
x
∈
R
{
-
π
4
+
k
π
,
k
∈
}...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 1 + sin 2 x với x ∈ R { - π 4 + k π , k ∈ } . Biết F(0)=1,F( π )=0, tính giá trị biểu thức P = F ( - π 12 ) - F ( 11 π 12 )
Câu 1 : Tính thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y = x3 , y = 0, x=0, x=1 quanh trục hoành
Câu 2 : Biết F(x) là một nguyên hàm của hàm f(x) = sin2x và F(π/4) = 1. Tính F(π/6)
1.
\(V=\pi\int\limits^1_0x^6dx=\dfrac{\pi x^7}{7}|^1_0=\dfrac{\pi}{7}\)
2.
\(F\left(x\right)=\int sin2xdx=-\dfrac{1}{2}cos2x+C\)
\(f\left(\dfrac{\pi}{4}\right)=1\Leftrightarrow-\dfrac{1}{2}cos\dfrac{\pi}{2}+C=1\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}cos2x+1\Rightarrow F\left(\dfrac{\pi}{6}\right)=\dfrac{3}{4}\)
Đúng 2
Bình luận (0)
Biết F(x) là nguyên hàm của hàm f(x)=sin2x và F ( π 4 ) = 1 . Tính F ( π 6 )
A. 5/4
B. 0
C. 1/2
D. 3/4
Biết F(x) là một nguyên hàm của hàm số f(x) sin2x và
F
π
4
1
Tính
F
π
6
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f(x) = sin2x và F π 4 = 1 Tính F π 6
Cho
F
(
x
)
cos
2
x
-
sin
x
+
C
là nguyên hàm của hàm số f(x). Tính
f
(
π
)
A.
f
(
π
)
-
3
B.
f
(
π
)
1
C.
f
(
π
)...
Đọc tiếp
Cho F ( x ) = cos 2 x - sin x + C là nguyên hàm của hàm số f(x). Tính f ( π )
A. f ( π ) = - 3
B. f ( π ) = 1
C. f ( π ) = - 1
D. f ( π ) = 0
Cho F(x) là nguyên hàm của hàm số
f
x
sin
2
x
và
F
π
4
1.
Tính
F
π
6
A.
F
π
6
1
2
B.
F
π
6...
Đọc tiếp
Cho F(x) là nguyên hàm của hàm số f x = sin 2 x và F π 4 = 1. Tính F π 6
A. F π 6 = 1 2
B. F π 6 = 0
C. F π 6 = 5 4
D. F π 6 = 3 4
Một nguyên hàm F(x) của hàm số
f
x
x
+
sin
2
x
sao cho đồ thị của hai hàm số F(x) và f(x) cắt nhau tại một điểm thuộc trục tung là A.
F
x
1
2
x
2
+
cos
2
x
+
1...
Đọc tiếp
Một nguyên hàm F(x) của hàm số f x = x + sin 2 x sao cho đồ thị của hai hàm số F(x) và f(x) cắt nhau tại một điểm thuộc trục tung là
A. F x = 1 2 x 2 + cos 2 x + 1
B. F x = 1 2 x 2 - cos 2 x + 1
C. F x = 1 2 x 2 − 1 2 cos 2 x + 1
D. F x = 1 2 x 2 − 1 2 cos 2 x − 1 2
Một nguyên hàm F(x) của hàm số
f
(
x
)
2
x
3
3
x
2
+
1
-
sin
2
x
khi F(0)1 là: A.
F
x
2
x
4
4
+
3...
Đọc tiếp
Một nguyên hàm F(x) của hàm số
f ( x ) = 2 x 3 = 3 x 2 + 1 - sin 2 x khi F(0)=1 là:
A. F x = 2 x 4 4 + 3 x 3 3 + x + 1 2 . cos 2 x + 1 2
B. F x = 2 x 4 4 - 3 x 3 3 + x + 1 2 . cos 2 x + 1 2
C. F x = 2 x 4 4 - 3 x 3 3 - x + 1 2 . cos 2 x + 1 2
D. F x = 2 x 4 4 - 3 x 3 3 + x + 1 2 . cos 2 x - 1 2
Một nguyên hàm F(x) của hàm số
f
(
x
)
2
x
3
-
3
x
2
+
1
-
sin
2
x
khi F(0)1 là:
Đọc tiếp
Một nguyên hàm F(x) của hàm số f ( x ) = 2 x 3 - 3 x 2 + 1 - sin 2 x khi F(0)=1 là:
