Tính tích phân I = ∫ 2 2 d x πx x 2 - 1
A. π 12
B. π 2 12
C. 1 12
D. Một đáp án khác
Cho tích phân I = ∫ 0 2 f ( x ) d x = 2 . Tính tích phân J = ∫ 0 2 3 f ( x ) - 2 d x
![]()
![]()
![]()
Cho (P) : y= \(x^2-4x+3\)và đường thẳng (d): y= m(x-2)-1. Tính tổng các giá trị của tham số m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt A, B sao cho diện tích tam giác IAB bằng 10 với điểm I(2;3).
Cho hàm số y = f x = x 2 k h i 0 ≤ x ≤ 2 - x k h i 1 ≤ x ≤
Tính tích phân I = ∫ 0 2 f x d x
A. 5 6
B. 1 3
C. 2
D. 3
Cho hàm số y = f ( x ) = x 2 k h i 0 ≤ x ≤ 1 2 - x k h i 1 ≤ x ≤ 2
Tính tích phân I= ∫ 0 2 f ( x ) d x
![]()
![]()
![]()
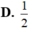
Cho hàm số y = f(x) liên tục trên [ 0 ; + ∞ ] và ∫ 0 x 2 f ( t ) d t = x sin x ( πx ) tính f(4)
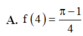
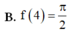
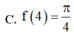
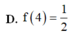
Phân tích đa thức thành nhân tử
x^8+x^6+x^4+x^2+1
Cho a^2+b^2=c^2+d^2=2016 và a×d = b×c=0
Tính(a×b)+(c×d)
Cho hàm số y = f(x) thỏa mãn ∫ 0 1 f ( x ) d x = 2 v à ∫ 1 5 f ( x ) d x = - 8 . Tính tích phân I = ∫ - 1 2 f 2 x - 3 d x .
A. I = -8
B. I = -2
C. I = -4
D. I = -6
Cho hàm số y=f(x) thỏa mãn ∫ 0 1 f ( x ) d x = 2 và ∫ 1 5 f ( x ) d x = - 8 . Tính tích phân I = ∫ - 1 2 f 2 x - 3 d x
![]()
![]()
![]()
![]()
Bài 1 phân tích đa thức thành nhân tử.
a , x^6 - y^6
b, x^2 + x + y^2 + y + 2xy
c, -x^2 + 5x + 2xy-5y -y^2
d, y^2 + 2yt-t^2 + 2vu + t^2 - u^2
\(x^6-y^6=\left(x^3-y^3\right)\left(x^3+y^3\right)=\left(x-y\right)\left(x^2+xy+y^2\right)\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(x^2+x+y^2+y+2xy=\left(x+y\right)^2+\left(x+y\right)=\left(x+y\right)\left(x+y+1\right)\)
\(-x^2+5x+2xy-5y-y^2=5\left(x-y\right)-\left(x-y\right)^2=\left(x-y\right)\left(5-x+y\right)\)
\(y^2+2yt-v^2+2vu+t^2-u^2==\left(y+t\right)^2-\left(v-u\right)^2=\left(y+t+v-u\right)\left(y+t-v+u\right)\)
tui làm tip 1 câu, các câu khác tt, bn p.an làm đúng mà bn k tích nên chẳng ai muon lam cho ke vo on dau
b) = (x+y)( x+y+1)
3A. Tính giá trị biểu thức: a) A = (x²-3x² + 3x)² -2(x²-3x² + 3x)+1 tại x= 11; b) B=(x-2y)(x² + 2xy + 4y²)-6xy(x-2y) tai x=3;y=; 5A. Phân tích đa thức thành nhân tử a) x² +1-2x²; c) y²-4x² + 4x-1; b)x²-y²-5y+5x; d) x (2+x)²-(x+2)+1-x² 6A. Phân tích đa thức thành nhân tử: (a) x² −8x+7; b) 2x² -5x+2; c) x²-5x² +8x-4; d) x² +64.