Tìm các số thực m để hàm số y= (m+2)x^3 +3x^2 +mx-5 có cực trị.
A. m ≠ 2 - 3 < m < 1
B. -3 < m < 1
C. m < - 3 m > 1
D. -2 < m < 1
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm tất cả các giá trị thực của m để hàm số y=mx^4 - (m+1)x^2 + 2m -1 có 3 cực trị
\(m=0\) không thỏa mãn
Với \(m\ne0\):
\(y'=4mx^3-2\left(m+1\right)x=2x\left(2mx^2-\left(m+1\right)\right)\)
Hàm có 3 cực trị khi:
\(\dfrac{m+1}{m}>0\Rightarrow\left[{}\begin{matrix}m< -1\\m>0\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m< -1\\m>0\end{matrix}\right.\)
TÌM THAM SỐ MLÀ SỐ THỰC CỦA ĐỂ HÀM SỐ Y = 1/3X³ - MX² + (M² – 4)X + 3 ĐẠT CỰC ĐẠI TẠI X = 3. A. M = -7 B. M = 1 C. MTÌM THAM SỐ MLÀ SỐ THỰC CỦA ĐỂ HÀM SỐ Y = 1/3X³ - MX² + (M² – 4)X + 3 ĐẠT CỰC ĐẠI TẠI X = 3. A. M = -7 B. M = 1 C. M = -1 D. M = 5. = -1 D. M = 5.
Câu 6. Tìm các giá trị thực của tham số \(m\) để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3.
A. \(m=1,m=5\)
B. \(m=5\)
C. \(m=1\)
D. \(m=-1\)
Ta có:
\(y'=x^2-2mx+m^2-4\)
\(y''=2x-2m,\forall x\in R\)
Để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3 thì:
\(\left\{{}\begin{matrix}y'\left(3\right)=0\\y''\left(3\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+5=0\\6-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=1,m=5\\m>3\end{matrix}\right.\Leftrightarrow m=5\)
=> B.
Cho hàm số f x = x 3 - 2 x - 1 x 2 + 2 - m x + 2 . Tìm tất cá các giá trị thực của tham số m để hàm số y = f x có 5 cực trị.
A. - 2 < m < 5 4
B. - 5 4 < m < 2
C. 5 4 ≤ m ≤ 2
D. 5 4 < m < 2
Chọn D.
Phương pháp:
Sử dụng tính chất đồ thị hàm đa thức bậc ba luôn cắt trục tung và đồ hàm số y=f(|x|) luôn nhận trục tung làm trục đối xứng để suy ra x=0 luôn là một cực trị của hàm y=f(|x|)
Lập luận để suy ra hàm f(x) có hai điểm cực trị dương phân biệt thì hàm số y=f(|x|) có 5 điểm cực trị
phân biệt.
Cách giải:
Nhận thấy rằng nếu x 0 là điểm cực trị của hàm số y=f(|x|) cũng là điểm cực trị của hàm số y=f(|x|) (1)
Lại thấy vì đồ thị hàm số y=f(|x|) nhận trục Oy làm trục đối xứng mà f(x) là hàm đa thứ bậc ba nên x=0 luôn là một điểm cực trị của hàm số y=f(|x|) (2)
Từ (1) và (2) suy ra để hàm số y=f(|x|) có 5 điểm cực trị thì hàm số
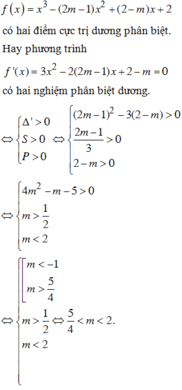

Cho hàm số f x = x 2 - 2 m - 1 x 2 + 2 - m x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y = f x có 5 cực trị.
A. 5 4 ≤ m ≤ 2
B. - 5 4 < m < 2
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số f x = x 3 - 2 m - 1 x 2 + 2 - m x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y = f x có 5 cực trị.
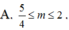
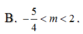
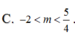
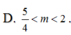
Cho hàm số f x = x 3 - 2 m - 1 x 2 + 2 - m x + 2 Tìm tất cá các giá trị thực của tham số m để hàm số y = f x có 5 cực trị.
A. - 2 < m < 5 4
B. - 5 4 < m < 2
C. 5 4 ≤ m ≤ 2
D. 5 4 < m < 2
Tìm tất các giá trị thực của tham số m để hàm số y = ( m + 2 ) x 3 + 3 x 2 + m x - 6 có 2 cực trị ?
A. m ∈ ( - 3 ; 1 ) / - 2 .
B. m ∈ ( - 3 ; 1 ) .
C. m ∈ ( - ∞ ; - 3 ) ∪ ( 1 ; + ∞ ) .
D. m ∈ - 3 ; 1 .
Chọn A
![]()
Hàm số có 2 cực trị ⇔ y ' = 0 có hai nghiệm phân biệt.
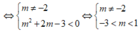
![]()