Tổng 3 số dương x;y;z biết x+y+z=xyz

Những câu hỏi liên quan
Tổng 3 số dương x,y,z biết x+y+x=xyz
Tổng 3 số dương x,y,z biết x+y+z=xyz
Do x,y,z có vai trò như nhau nên ta giả sử 0<x≤y≤z
Khi đó ta có xyz=x+y+z≤3z
⇒xy≤3
mà x,y là các số nguyên dương nên xyϵ{1;2;3}
Ta xét các trường hợp
+) TH1: xy=1 ⇒x=1;y=1⇒2+z=z, vô lí
+) TH2: xy=2⇒x=1;y=2 (do x≤y) ⇒3+z=2z⇔z=3
+) TH3: xy=3⇒x=1;y=3⇒4+z=3z⇔z=2
Nên ta có các cặp số (x;y;z) thỏa mãn đề bài là các hoán vị của (1;2;3)
Khi đó x+y+z=6
Đúng 0
Bình luận (0)
x=300
y=20
z=1
vì x+y+z=xyz
=>300+20+1=321
Đúng 0
Bình luận (0)
Tổng 3 số dương x,y,z biết x+y+z =x.y.z
tổng 3 số dương x,y,z biết x+y+z=xyz
tổng 3 số dương x, y, z
biết x+y+z=xyz
è, lớp 7 chứ, vio phải ko
tìm ra là 6
x=1;y=2;z=3
Đúng 0
Bình luận (0)
Tính tổng 3 số nguyên dương x;y;z biết x+y+z=xyz
Do x,y,z có vai trò như nhau nên ta giả sử 0<x≤y≤z
Khi đó ta có xyz=x+y+z < 3z
=> xy < 3
Mà x,y là các số nguyên dương nên xyϵ{1;2;3}
Ta xét các trường hợp
+) TH1: xy=1 =>x=1;y=1=>2+z=z, vô lí
+) TH2: xy=2=>x=1;y=2 (do x<y) >3+z=2z<=>z=3
+) TH3: xy=3=>x=1;y=3=>4+z=3z<=>z=2
Nên ta có các cặp số (x;y;z) thỏa mãn đề bài là các hoán vị của (1;2;3) Khi đó x+y+z=6
Đúng 0
Bình luận (0)
Do x,y,z có vai trò như nhau nên ta giả sử 0<x≤y≤z
Khi đó ta có xyz=x+y+z≤3z
⇒xy≤3
mà x,y là các số nguyên dương nên xyϵ{1;2;3}
Ta xét các trường hợp
+) TH1: xy=1 ⇒x=1;y=1⇒2+z=z, vô lí
+) TH2: xy=2⇒x=1;y=2 (do x≤y) ⇒3+z=2z⇔z=3
+) TH3: xy=3⇒x=1;y=3⇒4+z=3z⇔z=2
Nên ta có các cặp số (x;y;z) thỏa mãn đề bài là các hoán vị của (1;2;3)
Khi đó x+y+z=6
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tổng 3 số dương x,y,z biết x+y+z=x.y.z
6...........
Tik cho mk nha..............cảm ơn rất nhiều
Đúng 0
Bình luận (0)
Tổng 3 số dương x;y;z biết:
x+y+z=xyz
Do x,y,z có vai trò như nhau nên ta giả sử 0<x≤y≤z
Khi đó ta có xyz=x+y+z≤3z
⇒xy≤3
mà x,y là các số nguyên dương nên xyϵ{1;2;3}
Ta xét các trường hợp
+) TH1: xy=1 ⇒x=1;y=1⇒2+z=z, vô lí
+) TH2: xy=2⇒x=1;y=2 (do x≤y) ⇒3+z=2z⇔z=3
+) TH3: xy=3⇒x=1;y=3⇒4+z=3z⇔z=2
Nên ta có các cặp số (x;y;z) thỏa mãn đề bài là các hoán vị của (1;2;3)
Khi đó x+y+z=6
Đúng 0
Bình luận (0)
trời mk cũng đang làm bài đó nè, mk học thêm toán, thầy ra bài này mà mãi chả ai làm đc. bạn làm rùi cho mk xem ké vs, có thể sẽ đc thầy khen hề hề
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
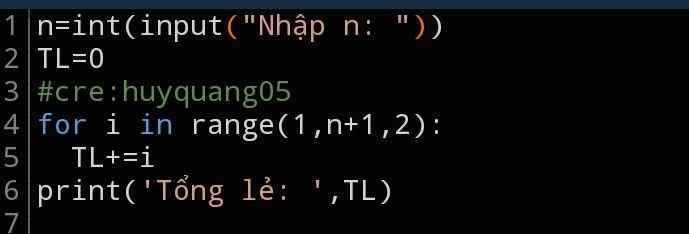
Bài 3. Tổng số lẻ Tên file: sumodd.***Cho số nguyên dương n. Em hãy tính tổng các số nguyên dương nhỏ hơn hoặc bằng n.Input: - một dòng duy nhất chứa số nguyên dương n.Output: - một dòng tổng của các số nguyên dương lẻ n.Ví dụ:InputOutput7161025
Đọc tiếp
Bài 3. Tổng số lẻ Tên file: sumodd.***
Cho số nguyên dương n. Em hãy tính tổng các số nguyên dương nhỏ hơn hoặc bằng n.
Input: - một dòng duy nhất chứa số nguyên dương n.
Output: - một dòng tổng của các số nguyên dương lẻ <= n.
Ví dụ:
Input | Output |
7 | 16 |
10 | 25 |
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++) if (i%2!=0) t+=i;
cout<<t;
return 0;
}
Đúng 0
Bình luận (0)