Dựa vào đồ thị của các hàm số y = x 3 và y = x 4 (H.26, H.27), hãy biện luận theo b số nghiệm của các phương trình x 3 = b v à x 4 = b .

Những câu hỏi liên quan
Cho đồ thị hàm số y = x\(^2\) -2x - 3 :
Dựa vào đồ thị biện luận theo m số nghiệm của phương trình: x^2 - 2x - 3 + m = 0
Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):
y = x/3(x+ 3)2 trong các khoảng (1/2; 3/2) và (3/2; 4)
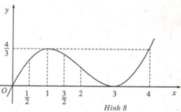
Tại x = 1 hàm số có giá trị lớn nhất bằng 4/3.
Tại x = 3 hàm số có giá trị nhỏ nhất bằng 0.
Xét dấu đạo hàm:
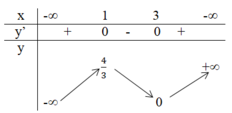
Đúng 0
Bình luận (0)
a, Lập bảng biến thiên, vẽ đồ thị (P) của hàm số : y = - x^2 + 4x - 3
b, Dựa vào đồ thị, hãy:
+ Tìm x để y > 0 ; y < 0;
+ Tìm max, min của hàm số trên đoạn [0;4].
+ Biện luận theo m số nghiệm của pt x^2 - 4x = m
+Tìm k để pt -x^2 + 4x = k có nghiệm thỏa mãn [-1;3]
a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |
Đúng 0
Bình luận (0)
a) Khảo sát hàm số y x3 + 3x2 + 1 (1)
b) Dựa vào đồ thị (C) của hàm số (1), biện luận về số nghiệm của phương trình
x2 (x + 3) m theo m
Đọc tiếp
a) Khảo sát hàm số y= x3 + 3x2 + 1 (1)
b) Dựa vào đồ thị (C) của hàm số (1), biện luận về số nghiệm của phương trình
x2 (x + 3) = m theo m
Cho parabol P : y= -x^2 + 4 x+5
a Khảo sát và vẽ đồ thị của hàm số P
b Dựa vào đồ thị P hãy biện luận số nghiệm phương trình x^2-4x-5-m
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:y −
x
3
+ 3x + 1b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:y
(
x
+
1
)
3
− 3x − 4c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
(
x
+
1...
Đọc tiếp
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
y = − x 3 + 3x + 1
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:
y = ( x + 1 ) 3 − 3x − 4
c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
( x + 1 ) 3 = 3x + m
d) Viết phương trình tiếp tuyến (d) của đồ thị (C’), biết tiếp tuyến đó vuông góc với đường thẳng
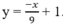
a)
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
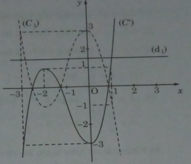
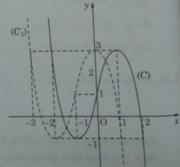
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
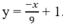
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 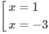
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.
Đúng 0
Bình luận (0)
a) Dựa vào đồ thị của hàm số ydfrac{1}{2}x^2�12�2(H.6.2), tìm x sao cho y8.b) Vẽ đồ thị của các hàm số y2x+1 và y2x^2 trên cùng một mặt phẳng tọa độ.
Đọc tiếp
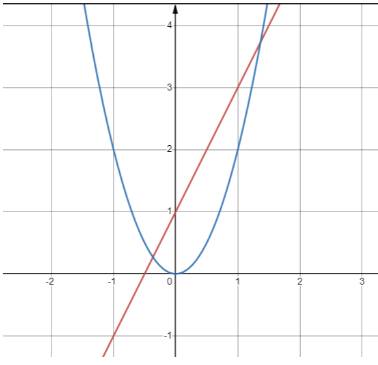
a) Dựa vào đồ thị của hàm số \(y=\dfrac{1}{2}x^2\)(H.6.2), tìm \(x\) sao cho \(y=8\).
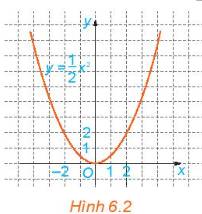
b) Vẽ đồ thị của các hàm số \(y=2x+1\) và \(y=2x^2\) trên cùng một mặt phẳng tọa độ.
a) Để \(y = 8 \Leftrightarrow \frac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = 4\) hoăc \(x = - 4\)
b) Vẽ đồ thị y=2x+1:
-Là đồ thị bậc nhất nên đồ thị là đường thẳng đi qua điểm có tọa độ (0; 1) và
(-1; -1)
Vẽ đồ thị \(y = 2{x^2}\)
- Đi qua điểm (1; 2) ; (-1; 2);(0;0)
Đúng 0
Bình luận (0)
cho hàm sô y= x2 -4x+3(P)
a, vẽ đồ thị (P') và lập bảng biến thiên của y= | -x2 +4x-3|
b, dựa vào đồ thị (P') , biện luận theo m số nghiệm phương trình | x2-4x+3|-m-1=0
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi y f(x), y g(x) và y h(x) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian x. Qua biểu đồ, hãy:Tìm tập xác định của mỗi hàm số đã nêu.
Đọc tiếp
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi y = f(x), y = g(x) và y = h(x) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian x. Qua biểu đồ, hãy:
Tìm tập xác định của mỗi hàm số đã nêu.
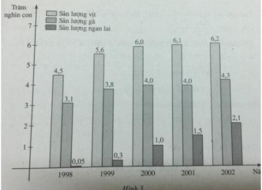
Tập xác định của cả ba hàm số y = f(x), y = g(x) và y = h(x) là:
D = {1998, 1999, 2000, 2001, 2002}
Đúng 0
Bình luận (0)












