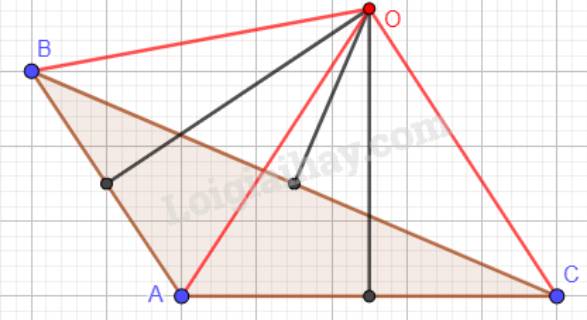
Vẽ đường tròn đi qua ba đỉnh của tam giác ABC trong các trường hợp sau:
A ^ , B ^ , C ^ đều nhọn
A ^ = 90 o
A ^ > 90 o
54/SGK lớp 7 tập 2 hình học
Vẽ đường tròn đi qua 3 đỉnh của tam giác ABC trong các trường hợp sau:
a) Góc A,B,C đều nhọn
b) Góc A=90 độ
c) Góc A lớn hơn 90 độ
Vẽ đường tròn đi qua 3 đỉnh của tam giác ABC trong các trường hợp sau
a) \(\widehat{A},\widehat{B},\widehat{C}\) đều nhọn
b) \(\widehat{A}=90^0\)
c) \(\widehat{A}>90^0\)
Hướng dẫn:
Đường tròn đi qua ba dỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó. Đẻ vẽ đường tròn ngoại tiếp ta cần xác định tâm của đường tròn đó. Muốn xác định tâm ta vẽ hai đường trung trực và giao điểm hai đường trung trực ( cũng là giao điểm của ba trung trực cần tìm)
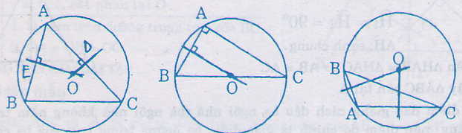
Nhận xét:
- Nếu tam giác có ba góc đều nhọn thì tâm đường tròn ngoại tiếp nằm trong tam giác.
- Nếu tam giác có góc vuông thì tâm đường tròn nằm trên cạnh huyền ( tâm là trung điểm của cạnh huyền)
- Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp nằm ngoài tam giác
Đường tròn đi qua ba dỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó. Đẻ vẽ đường tròn ngoại tiếp ta cần xác định tâm của đường tròn đó. Muốn xác định tâm ta vẽ hai đường trung trực và giao điểm hai đường trung trực ( cũng là giao điểm của ba trung trực cần tìm)

Nhận xét:
- Nếu tam giác có ba góc đều nhọn thì tâm đường tròn ngoại tiếp nằm trong tam giác.
- Nếu tam giác có góc vuông thì tâm đường tròn nằm trên cạnh huyền ( tâm là trung điểm của cạnh huyền)
- Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp nằm ngoài tam giác
Đường tròn đi qua ba dỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó. Đẻ vẽ đường tròn ngoại tiếp ta cần xác định tâm của đường tròn đó. Muốn xác định tâm ta vẽ hai đường trung trực và giao điểm hai đường trung trực ( cũng là giao điểm của ba trung trực cần tìm)

Nhận xét:
- Nếu tam giác có ba góc đều nhọn thì tâm đường tròn ngoại tiếp nằm trong tam giác.
- Nếu tam giác có góc vuông thì tâm đường tròn nằm trên cạnh huyền ( tâm là trung điểm của cạnh huyền)
- Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp nằm ngoài tam giác
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
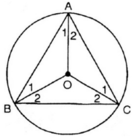
Do ![]()
nên số đo các cung nhỏ AB,BC và AC là:![]()
Suy ra,số đo các cung lớn AB, AC và BC là: 3600 - 1200 = 2400
Chứng minh rằng tập hợp các điểm cách đều ba đỉnh của một tam giác ABC là đường vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn ngoại tiếp tam giác ABC.
- Lấy một điểm M bất kì trong không gian sao cho MA = MB = MC. Từ M kẻ MO vuông góc với mp(ABC). Các tam giác vuông MOA, MOB, MOC bằng nhau, cho ta OA = OB = OC.
- Suy ra O là tâm đường tròn ngoại tiếp tam giác ABC. Vậy các điểm M cách đều ba đỉnh của tam giác ABC nằm trên đường thẳng d đi qua tâm O của đường tròn ngoại tiếp tam giác ABC và vuông góc với mp(ABC). Ngược lại, lấy một điểm M' ∈ d, nối M'A, M'B, M'C.
- Do M'O chung và OA = OB = OC nên các tam giác vuông M'OA, M'OB, M'OC bằng nhau, cho ta M'A = M'B = M'C.
- Tức là điểm M' cách đều ba đỉnh A, B, C của tam giác ABC.
- Kết luận : Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là đường thẳng vuông góc với mp(ABC) và đi qua tâm của đường tròn ngoại tam giác ABC.
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
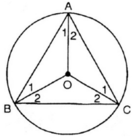
Vì tam giác ABC là tam giác đều nên 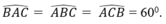
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC
![]()
* Xét tam giác AOB có:
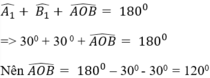
* Tượng tự ta được: ![]()
a) Ta có : ^A = ^B = ^C =60^o ( gt )
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC
Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o
=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o
Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o
b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :
\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)
\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)
cho tam giác ABC . qua đỉnh A vẽ đường thẳng a song song với BC . quá đỉnh B vẽ đường thẳng b song song với AC , a và b cắt nhau tại O . hãy xác định một góc đình O co so đó bằng góc C của tam giác ABC
vẽ tiếp hình trong trường hợp tam giác ABC có góc C tù
vẽ hình đối xứng của tam giác abc qua điểm o cho trước trong các trường hợp sau a) o trùng với trọng tâm g của tam giác b) o trùng với đỉnh a của tam giác
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua ba đỉnh A, B, C.
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
b) Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
a) Ta có: 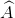 =
= 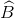 =
= 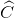 =
= 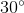 (gt)
(gt)
Suy ra:  =
= 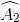 =
= 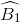 =
= 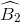 =
= 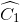 =
= 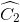 =
= 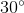 .
.
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của bà cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC.
Suy ra: 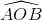 =
= 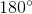 - (
- ( +
+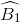 ) =
) = 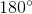 -
- 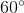 =
= 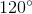
Tương tự ta suy ra 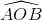 =
= 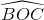 =
= 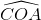 =
= 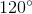 .
.
b) Từ 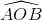 =
= 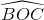 =
= 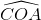 =
= 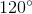 ta suy ra:
ta suy ra:
Cung ABC = BCA = CAB = 240º
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
a) Tam giác ABC nhọn:
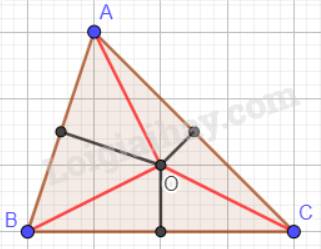
b) Tam giác ABC vuông tại A:
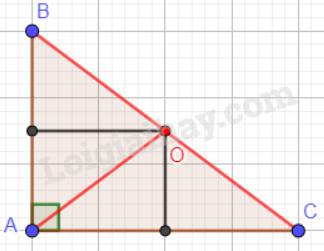
c) Tam giác ABC có góc A tù: