Cho hình 57.
Chứng minh NS ⊥ LM
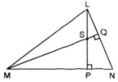
Hình 57
Cho hình 57 :
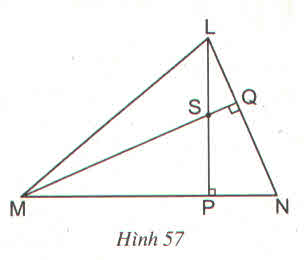
a) Chứng minh \(NS\perp LM\)
b) Khi \(\widehat{LNP}=50^0\), hãy tính góc MSP và góc PSQ
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay SN ⊥ ML
Cho hình 57.
Khi góc LNP = 50o, hãy tính góc MSP và góc PSQ.
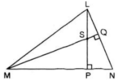
Hình 57
+ Ta có : trong tam giác vuông, hai góc nhọn phụ nhau nên :
ΔNMQ vuông tại Q có:

Cho hình 57, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC
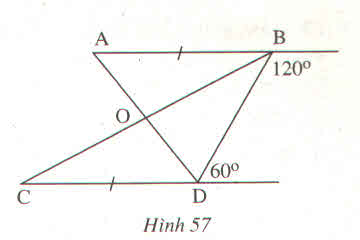
Ta có: góc B + góc D = 1200 + 600 = 1800
Mà hai góc này TCP
=> AB // CD
Xét tam giác ABO và tam giác CDO có:
AB = CD (GT)
ABC = BCD (AB // CD)
BAD = ADC (AB // CD)
=> tam giác ABO = tam giác CDO
=> AO = OD
=> O là trung điểm AD
Ta có: tam giác ABO = tam giác CDO
=> BO = OC
=> O là trung điểm BC
Chứng minh rằng: 106 - 57 chia hết cho 59
106 - 57 = (2.5)6 - 56.5 = 26.56 - 56.5=56.(26 - 5)=56.59⋮ 59
Cho A =7 + 72 + 73 + ... + 7119 + 7120. Chứng minh chia hết cho 57
\(A=7+7^2+7^3+...+7^{120}\\ A=\left(7+7^2+7^3\right)+...+\left(7^{118}+7^{119}+7^{120}\right)\\ A=7\times\left(1+7+7^2\right)+...+7^{118}\times\left(1+7+7^2\right)\\ A=7\times57+7^4\times57+...+7^{118}\times57\\ A=57\times\left(7+7^4+...+7^{118}\right)\\ \Rightarrow A⋮57\)
7.7 mũ2.7 mũ3.7 mũ4......7 mũ120 . chứng minh chia hết cho 57
Cho:
A= 7+7²+7³+...+7¹¹⁹+7¹²⁰
chứng minh A chia hết cho 57
\(A=7+7^2+7^3+...+7^{119}+7^{120}\)
\(\Rightarrow7A=7^2+7^3+7^4+...+7^{120}+7^{121}\)
\(\Rightarrow7A-A=\left(7^2+7^3+...+7^{120}+7^{121}\right)-\left(7+7^2+...+7^{119}+7^{120}\right)\)
\(\Rightarrow6A=7^2+7^3+...+7^{120}+7^{121}-7-7^2-...-7^{119}-7^{120}\)
\(\Rightarrow6A=7^{121}-7\)
\(\Rightarrow A=\dfrac{7^{121}-7}{6}\)
Chứng minh: 7^20+49^11+343^7 chia hết cho 57 ?
7^20 + 49^11 + 343^7 = ( 7^1 )^20 + ( 7^2 )^11 + ( 7^3 )^7
=7^20 + 7^21 + 7^22 = 7^20 ( 1 + 7 + 7^2 ) = 720.57 Vì 57 chia hết cho 57 nên 7^20 .57 chia hết cho 57 => 7^20 + 49^11 + 343^7 chia hết cho 57
chứng minh 3^5371+57^2016+92^2017 chia hết cho 10