Cho biết (4m+5)chia hết cho 23.Chứng minh rằng (7m+3)chia hết cho 23

Những câu hỏi liên quan
cho x,ythuoc so nguyên biết 3x+10 chia hết cho 23 , chứng minh rằng x+11y chia hết cho 23
Cho
A
2
+
2
2
+
2
3
+
.
.
.
+
2
20
. Chứng minh rằng:a) A chia hết cho 2;b) A chia hết cho 3;c) A chia hết cho 5.
Đọc tiếp
Cho A = 2 + 2 2 + 2 3 + . . . + 2 20 . Chứng minh rằng:
a) A chia hết cho 2;
b) A chia hết cho 3;
c) A chia hết cho 5.
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:

![]()
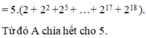
Đúng 1
Bình luận (0)
4₁ A= 2 +2²³ +2 ² + + 220
a₁ A = 2₁ [1 + 2 +2²¹ +. +2¹2):2 Vay A chia hết choi
b₁ A = 2 + 2² +2²+ + 220 (2 +2²) + (2 ² + 2 9) + . + (219+220)
= 2₁ (1 + 2) + 2² (2+1). .. +2 19 (2+1) + = 2₁3 + 2³.3 + ..+ 219.3.
= (2+2 ³+ + 219) 3:3 Vậy A chia hết cho 3 A = 2 + 2 ² + 2³ + 2ª +. 20 + 2.9+ +2
2+2 ³ + 2² +2²4 + + 218 + 720 +2²³ +2²+ +218 +220 2. (2 +2²) + 2² (1+2²) +.. + 218 ( 1 +2²) = 2 5 +2²5 + + 218 5. 12 +2° + 2 ... +218 ) 5 : 5.
vậy A chia hết cho 5
Cho x , y là hai số nguyên biết 3x + 10 chia hết cho 23 chứng minh rằng x + 11y chia hết cho 23
vì x chia hết cho 23 và 11 nhân y cũng chia hết cho 23
Đúng 0
Bình luận (0)
cho c = 2 + 2 mũ 3 + 2 mũ 5 + ....+ 2 mũ 23 chứng minh rằng
a, c chia hết cho 21 b, c chia hết cho 10
`#3107.101107`
a,
\(C=2+2^3+2^5+...+2^{23}\)
\(=\left(2+2^3+2^5\right)+\left(2^5+2^7+2^9\right)+...+\left(2^{19}+2^{21}+2^{23}\right)\)
\(=2\left(1+2^2+2^4\right)+2^5\cdot\left(1+2^2+2^4\right)+...+2^{19}\cdot\left(1+2^2+2^4\right)\)
\(=\left(1+2^2+2^4\right)\cdot\left(2+2^5+...+2^{19}\right)\)
\(=21\cdot\left(2+2^5+...+2^{19}\right)\)
Vì \(21\text{ }⋮\text{ }21\)
\(\Rightarrow21\left(2+2^5+...+2^{19}\right)\text{ }⋮\text{ }21\)
Vậy, \(C\text{ }⋮\text{ }21\)
b,
\(C=2+2^3+2^5+...+2^{23}\)
\(=\left(2+2^3\right)+\left(2^5+2^7\right)+...+\left(2^{21}+2^{23}\right)\)
\(=\left(2+2^3\right)+2^4\cdot\left(2+2^3\right)+...+2^{20}\cdot\left(2+2^3\right)\)
\(=\left(2+2^3\right)\cdot\left(1+2^4+...+2^{20}\right)\)
\(=10\cdot\left(1+2^4+...+2^{20}\right)\)
Vì \(10\text{ }⋮\text{ }10\)
\(\Rightarrow10\cdot\left(1+2^4+...+2^{20}\right)\text{ }⋮\text{ }10\)
Vậy, \(C\text{ }⋮\text{ }10.\)
Đúng 5
Bình luận (0)
a) c = 2 + 2³ + 2⁵ + ... + 2¹⁹ + 2²¹ + 2²³
= (2 + 2³ + 2⁵) + (2⁷ + 2⁹ + 2¹¹) + ... + (2¹⁹ + 2²¹ + 2²³)
= 2.(1 + 2² + 2⁴) + 2⁷.(1 + 2² + 2⁴) + ... + 2¹⁹.(1 + 2² + 2⁴)
= 2.21 + 2⁷.21 + ... + 2¹⁹.21
= 21.(2 + 2⁷ + ... + 2¹⁹) ⋮ 21
Vậy c ⋮ 21
b) c = 2 + 2³ + 2⁵ + 2⁷ + ... + 2²¹ + 2²³
= (2 + 2³) + (2⁵ + 2⁷) + ... + (2²¹ + 2²³)
= 10 + 2⁴.(2 + 2³) + ... + 2²⁰.(2 + 2³)
= 10 + 2⁴.10 + ... + 2²⁰.10
= 10.(1 + 2⁴ + ... + 2²⁰) ⋮ 10
Vậy c ⋮ 10
Đúng 2
Bình luận (0)
A = 2+22+23+....+220 .
CHỨNG MINH RẰNG :
a) A chia hết cho 3
b) A chia hết cho 5
a) \(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(A=2\cdot\left(1+3\right)+2^3\cdot\left(1+3\right)+...+2^{59}\cdot\left(1+3\right)\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\)
Vậy A chia hết cho 3
________
\(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\)
Vậy A chia hết cho 5
Đúng 1
Bình luận (0)
7)Chứng minh rằng :
a) abcabc chia hết cho 7,11,13
b) abcdeg chia hết cho 23 và 29 , biết rằng abc=2.deg
8)Chứng minh rằng nếu ab+cd+eg chia hết cho 11 thì abcdeg chia hết cho 11
7)a) abcabc : abc = 1001
abcabc = 1001 x abc . Mà 1001 chia hết cho 7; 11; 13 nên 1001 x abc chia hết cho 7; 11; 13 . Vậy abcabc chia hết cho 7; 11; 13 ( đpcm)
b .Vì abc = 2 . deg nên abcdeg : deg = 2001
abcdeg = 2001 x deg. Do 2001 chia hết cho 23 và 29 nên 2001 x deg chia hết cho 23 và 29 . Vậy abcdeg chia hết cho 23 và 29 ( đpcm)
Đúng 0
Bình luận (0)
Ta có :
abcabc = 1000abc + abc
= 1001 . abc
= 7 . 11 . 13 . abc chia hết cho 7 ; 11 ; 13
Đúng 0
Bình luận (0)
Cho B=23!+19!-15!
Chứng minh rằng B chia hết cho 11
chia hết cho 110
chia hết cho 5
+, Ta có:
\(B=23!+19!-15!\)
\(B=\left(1\times2\times...\times11\times...\times23\right)+\left(1\times2\times...\times11\times...\times19\right)-\left(1\times2\times...\times11\times...\times15\right)\)
\(B=11\times\left[\left(1\times2\times...\times10\times12\times...\times23\right)+\left(1\times2\times...\times10\times12\times...\times19\right)-\left(1\times2\times...\times10\times12\times...\times15\right)\right]\)
\(\Rightarrow B⋮11\)
+, Ta có:
\(B=23!+19!-15!\)
\(B=\left(1\times2\times...\times10\times11\times...\times23\right)+\left(1\times2\times...\times10\times11\times...\times19\right)-\left(1\times2\times...\times10\times11\times...\times15\right)\)
\(B=11\times10\times\left[\left(1\times2\times...\times9\times12\times...\times23\right)+\left(1\times2\times...\times9\times12\times...\times19\right)-\left(1\times2\times...\times9\times12\times...\times15\right)\right]\)
\(B=110\times\left[\left(1\times2\times...\times9\times12\times...\times23\right)+\left(1\times2\times...\times9\times12\times...\times19\right)-\left(1\times2\times...\times9\times12\times...\times15\right)\right]\)
\(\Rightarrow B⋮110\)
+,Ta có:
\(B=23!+19!-15!\)
\(B=\left(1\times2\times...\times5\times...\times23\right)+\left(1\times2\times...\times5\times...\times19\right)-\left(1\times2\times...\times5\times...\times15\right)\)
\(B=5\times\left[\left(1\times2\times...\times4\times6\times...\times23\right)+\left(1\times2\times...\times4\times6\times...\times19\right)-\left(1\times2\times...\times4\times6\times...\times15\right)\right]\)
\(\Rightarrow B⋮5\)
~ Chúc bạn học tốt ~!
Câu hỏi : Chứng minh rằng với mọi số nguyên x,y thì
a) 2.x^2 + 3.y chia hết cho 17 khi và chỉ khi 9.x^2 + 5.y chia hết cho 17
b) 5.x^2 - 4.y chia hết cho 23 khi và chỉ khi 3.x^2 - 7.y chia hết cho 23
Cho a,b thuộc số tự nhiên, 7a+3b chia hết cho 23 .Chứng minh rằng 4a+5b chia hết cho 23
Ta có: 7a+3b⋮23⇒6(7a+3b)⋮237a+3b⋮23⇒6(7a+3b)⋮23
⇒6(7a+3b)+(4a+5b)⋮23⇒6(7a+3b)+(4a+5b)⋮23
⇒46a+23b⋮23⇒23(2a+b)⋮23⇒46a+23b⋮23⇒23(2a+b)⋮23(Đúng)
Vậy 4a+5b⋮23

























