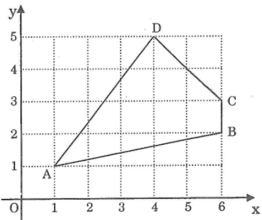
Tính độ dài các đoạn thẳng AB, BC, CD và DA trên hình dưới.
Xét ∆AHB và ∆ CKD có:HB = KD (= 1 ô)AHBˆ = CKDˆAH = CK (= 3 ô)=> ∆AHB = ∆CKD(c.g.c)=> AB = CD (cạnh tương ứng)Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)suy ra BC=AD.b) Xét ∆ABD và ∆CDB có:AB = CD (cmt)BC = AD (cmt)BD chung.=> ∆ABD = ∆CDB (c.c .c)=> ABDˆ = CDBˆMà hai góc này ở vị trí so le trongVậy AB // CD (đpcm)
chả bt có khớp ko chứ lười đọc quá
a) Sắp xếp độ dài các đoạn thẳng AB, BC, CD, DA trong hình 46 theo thứ tự giảm dần ( SGK trang 119 )
b) Tính chu vi hình ABCD ( tức là tính AB + BC + CD + DA ).
Tính độ dài các đoạn thẳng AB, BC, CD, DA trên hình 63
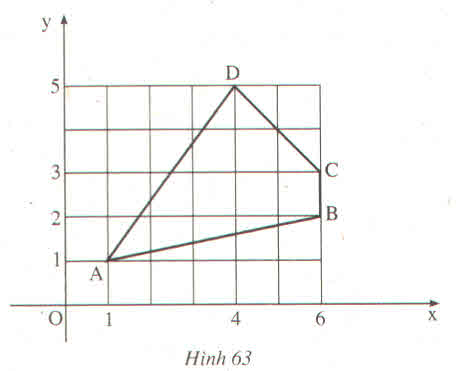
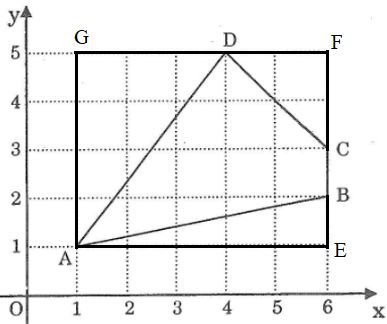
Ta có: \(BC=1.\)
+ Xét \(\Delta ABE\) vuông tại E có:
\(AB^2=AE^2+BE^2\) (định lí Py - ta - go).
=> \(AB^2=5^2+1^2\)
=> \(AB^2=25+1\)
=> \(AB^2=26\)
=> \(AB=\sqrt{26}\) (vì \(AB>0\)).
+ Xét \(\Delta CDF\) vuông tại F có:
\(CD^2=DF^2+CF^2\) (định lí Py - ta - go).
=> \(CD^2=2^2+2^2\)
=> \(CD^2=4+4\)
=> \(CD^2=8\)
=> \(CD=\sqrt{8}\) (vì \(CD>0\)).
+ Xét \(\Delta ADG\) vuông tại G có:
\(AD^2=AG^2+DG^2\) (định lí Py - ta - go).
=> \(AD^2=4^2+3^2\)
=> \(AD^2=16+9\)
=> \(AD^2=25\)
=> \(AD=5\) (vì \(AD>0\)).
Vậy \(AB=\sqrt{26};BC=1;CD=\sqrt{8};AD=5.\)
Chúc bạn học tốt!
Ta tính được : AB = \(\sqrt{26}\) ; CD = \(\sqrt{8}\) ; BC = 1 ; DA = 5
Tính độ dài các đoạn thẳng AB, BC, CD và DA trên hình dưới:
Mn giải cụ thể giúp mk vs! Mơn trc!
Hình đâu bạn ei
Hình đâu bạn
Với đề như này phải có hình với giải được
Bạn ko cho hình thì mình cũng chịu rồi bạn ạ
Học Tốt !@
Sắp xếp độ dài các đoạn thẳng AB, BC, CD, DA trong hình 46 theo thứ tự giảm dần.
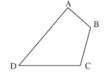
Hình 46
Sử dụng thước kẻ đo độ dài các đoạn thẳng trong hình 46. Ta được:
AB = 12 mm, BC = 16 mm, CD = 25 mm, DA = 30 mm suy ra: AB < BC < CD < DA
Vậy thứ tự giảm dần về độ dài các đoạn thẳng là: DA, CD, BC, AB.
trên một đường thẳng cho 4 điểm A,B,C,D theo thứ tự đó. Biết AB = 1,5 cm, độ dài đoạn BC bằng 2 lần độ dài đoạn AB và độ dài đoạn CD bằng 2 lần độ dài đoạn BC. tính độ dài các đoạn BC, CD
,
Hai đoạn thẳng AC, BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn thẳng. Tính các độ dài AB,BC,CD,DA biết AC = 12 cm; BD = 16cm
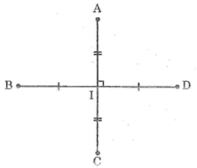
Gọi I là giao điểm của AC và BD
Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm
Vì I là trung điểm của BD nên IB = ID = BD/2=8cm
Áp dụng định lí pitago vào tam giác vuông AIB ta có:
AB2=IA2+IB2
AB2=62+82=36+64=100
Vậy AB = 10 cm
Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)
Suy ra: AD = BC = CD = AB = 10cm
Hai đoạn thẳng AC, BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn thẳng. Tính các độ dài AB, BC, CD, DA biết AC = 12cm, BD = 16cm ?
Gọi M là giao của AC và BD
Ta có: AC = 12 cm
M là trung điểm AC => AM = MC = 6 cm
Ta có: BD = 16 cm
M là trung điểm BD => BM = MD = 8 cm
Xét hai tam giác vuông ABM và CBM có:
BM: cạnh chung
AM = CM (cmt)
=> tam giác ABM = tam giác CBM (1)
Xét hai tam giác CBM và ADM có:
AM = MC (cmt)
BMC = AMD (đđ)
BM = MD (cmt)
=> tam giác CBM = tam giác ADM (2)
Xét hai tam giác vuông ADM và CDM có:
CM: chung
AM = MC (cmt)
=> tam giác ADM = tam giác CDM (3)
Từ (1);(2);(3)
=> bốn tam giác ABM; BCM; CAM; DAM bằng nhau
=> AB = BC = CD = DA
Ta có: tam giác ABM vuông
theo định lí pytago ta có:
AB2 = AM2 + BM2
=> AB2 = 62 + 82
=> AB2 = 100
=> AB = 10 cm
Có: AB = BC = CD = DA = 10 cm
Vậy: AB = 10 cm
BC = 10 cm
CD = 10 cm
DA = 10 cm.
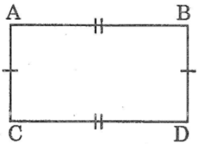
So sánh các đoạn thẳng AB, BC, CD, DA trong hình dưới rồi đánh dấu cho các đoạn thẳng bằng nhau.

Dùng thước chia khoảng để đo độ dài các đoạn. Ta có:
AB = 37mm
CD = 37mm
AC = 20mm
BD = 20mm
Suy ra: AB = CD; AC = BD