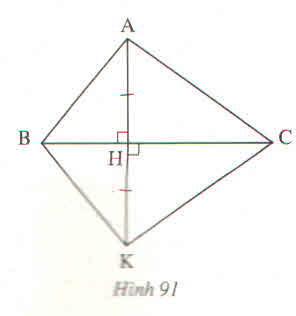
Tìm các tia phân giác trên hình 91
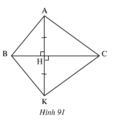
Tìm các tia phân giác trên hình 91. Hãy chứng minh điều đó ?
Giải:
∆AHB và ∆KBH có
AH=KH(gt)
\(\widehat{AHB}\)=\(\widehat{KHM}\)
BH cạnh chung .
nên ∆AHB=∆KBH(c.g.c)
suy ra: \(\widehat{ABH}\)=\(\widehat{KBH}\)
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC(c.g.c)
Suy ra: \(\widehat{ACH}\)=\(\widehat{KCH}\)
Vậy CH là tia phân giác của góc C.
- Xét ΔAHB và ΔKBH có:
BH cạnh chung
AH = KH
Nên ΔAHB = ΔKBH
Vậy BH là tia phân giác của góc B
- Tương tự ΔAHC = ΔKHC (c.g.c)
Vậy CH là tia phân giác của góc C.
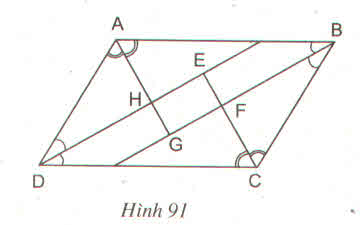
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
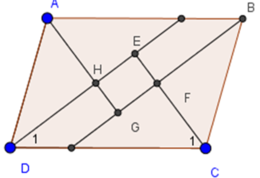
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như hình 91. Chứng minh rằng EFGF là hình chữ nhật
Bài giải:
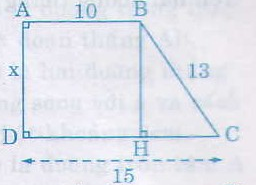
Kẻ BH ⊥ CD
Suy ra DH = 10
Nên HC = 5.
Do đó
BH2 = 132 - 52 = 169 – 25 =144
=> BH = 12
Vậy x = 12.
cho góc bẹt xoy trên cùng một nửa mp bờ chứa xy và hai tia Oz, Ot sao cho góc xoy= 50 độ, góc yot= 65 độ
a) tìm trên hình vẽ các tia thuộc cùng 1 nửa mp có bờ chứa tia Oz , tìm các tia thuộc 2 nửa m đối nhau có bờ chứa tia ot
b)Chỉ ra các cặp góc kề nhau trên hình vẽ
c) tính góc zoy. Chứng tỏ ot là tia phân giác của góc zoy
Trên cùng một nửa mặt phẳng bờ chứa tia Oa. Vẽ tia Ob, Oc, Od sao cho góc aOb = 40 độ. góc aOc = 80 độ, góc aOd= 120 độ. Tìm các tia phân giác có trong hình
(Bạn tự vẽ hình!)
- Tia phân giác đầu tiên là \(Ob\)
Giải thích: Ta có: \(\widehat{cOb}+\widehat{bOa}=\widehat{cOa}\)
\(\Rightarrow\widehat{cOb}=\widehat{cOa}-\widehat{bOa}=80-40=40\)độ
Vậy: \(\widehat{cOb}=\widehat{bOa}=\frac{\widehat{cOa}}{2}\)
Mà \(Ob\)nằm giữa \(Oc;Oa\Rightarrow..\)
- Tia phân giác thứ 2 là \(Oc\)
Giải thích: Ta có: \(\widehat{dOb}+\widehat{bOa}=\widehat{dOa}\)
\(\Rightarrow\widehat{dOb}=\widehat{dOa}-\widehat{bOa}=120-40=80\)độ
\(\widehat{dOc}+\widehat{cOb}=\widehat{dOb}\)
\(\Rightarrow\widehat{dOc}=\widehat{dOb}-\widehat{cOb}=80-40=40\)độ
Vậy: \(\widehat{dOc}=\widehat{cOb}=\frac{\widehat{dOb}}{2}\)
Mà \(Oc\)nằm giữa \(Od;Ob\Rightarrow..\)
cho tam giác ABC. Trên tia đối của tia AB lấy E, trên tia đối của tia AC lấy D. Các tia phân giác của các góc ACB và AED cắt nhau ở S. CMR: góc ESC = ( góc ABD + góc ADE) : 2
( cho em xin hình vẽ nữa ạ )Cho hai đoạn thẳng AB và CD vuông góc với nhau tại trung điểm của mỗi đoạn. Kẻ các đoạn thẳng AC, CB, BD, DA. Tìm các tia phân giác của các góc (khác góc bẹt) trên hình.
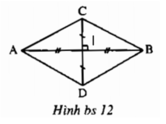
+ Gọi giao điểm của AB và CD là I. Theo giả thiết I là trung điểm của CD và AB.
+) Xét tam giác ACI và tam giác ADI có:
AI chung
CI = DI (vì I là trung điểm của CD).
∠AIC = ∠ DIA = 90º ( vì AB vuông góc với CD tại I).
Suy ra: ∆ ACI = ∆ ADI (c.g.c)
Suy ra: ∠CAI = ∠ ADI ( hai góc tương ứng).
Do đó, AB là tia phân giác của góc ∠CAD .
+) Chứng minh tương tự ta có: CD là tia phân giác của góc C, BA là tia phân giác của góc B, DC là tia phân giác của góc D.
BT1: cho xOy có Ot là tia phân giác , C thuộc Om ( C khác O ). Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB.Chứng minh:
a,tam giác OAC = tam giác OBC
b,góc OAC = góc OBC và CA=CB
BT2: cho tam giác ABC,kẻ AH vuông góc với BC ( H thuộc BC ). trên tia đối của tia HA , lấy điểm K sao cho HK = HA . Nối KB,KC . tìm các cặp tam giác bằng nhau trong hình vẽ
ai nhanh mk tick ( vẽ hình luôn nha)
Xét tam giác AOM và tam giác BOM có:
AO = BO (gt)
AOM = BOM (OM là tia phân giác của AOB)
OM chung
=> Tam giác AOM = Tam giác BOM (c.g.c)
=> AM = BM (2 cạnh tương ứng)
=> M là trung điểm của AB
=> OM là đường trung tuyến của tam giác OAB cân tại O (OA = OB)
=> OM là đường trung trực của tam giác OAB cân tại O
=> OM _I_ AB
Tam giác NAB có NA vừa là đường cao, vừa là đường trung trực
=> Tam giác NAB cân tại N
=> NA = NB