Giải các phương trình sau bằng cách đặt ẩn số phụ 2 x 2 + x - 2 2 +10 x 2 +5x -16 =0

Những câu hỏi liên quan
Giải các phương trình sau bằng cách đặt ẩn số phụ x - x - 1 -3 = 0
Đặt m = x - 1 .Điều kiện : m ≥ 0, x ≥ 1
Ta có : x - x - 1 -3 = 0 ⇔ (x -1) - x - 1 -2 =0
⇔ m 2 -m - 2 =0
Phương trình m 2 -m - 2 = 0 có hệ số a = 1, b = -1 , c = -2 nên có dạng
a – b + c = 0
Suy ra : m 1 = -1 (loại) , m 2 = -(-2)/1 = 2
Với m =2 ta có: x - 1 =2 ⇒ x -1 =4 ⇔ x =5
Giá trị của x thỏa mãn điều kiện bài toán
Vậy phương trình đã cho có 1 nghiệm : x=5
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng cách đặt ẩn số phụ ( x 2 -3x +4)( x 2 -3x +2) =3
Đặt m= x 2 -3x +2
Ta có: ( x 2 -3x +4)( x 2 -3x +2) =3
⇔ [( x 2 -3x +2 +2)( x 2 -3x +2) -3 =0
⇔ x 2 - 3 x + 2 2 +2( x 2 -3x +2) -3 =0
⇔ m 2 +2m -3 =0
Phương trình m 2 +2m -3 = 0 có hệ số a = 1, b = 2 , c = -3 nên có dạng
a +b+c=0
suy ra : m 1 =1 , m 2 =-3
Với m 1 =1 ta có: x 2 -3x +2 =1 ⇔ x 2 -3x +1=0
∆ = - 3 2 -4.1.1 = 9 -4 =5 > 0
∆ = 5
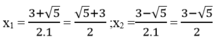
Với m 2 =-3 ta có: x 2 -3x +2 =-3 ⇔ x 2 -3x +5=0
∆ = - 3 2 -4.1.5 = 9 -20 =-11 < 0.Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
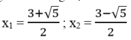
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng cách đặt ẩn số phụ x 2 + 3 x - 1 2 +2( x 2 +3x -1) -8 =0
Đặt m = x 2 +3x -1
Ta có: x 2 + 3 x - 1 2 +2( x 2 +3x -1) -8 =0 ⇔ m 2 +2m -8 =0
∆ ’ = 1 2 -1.(-8) =1 +8 =9 > 0
∆ ' = 9 =3
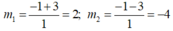
Với m = 2 thì : x 2 +3x - 1 = 2 ⇔ x 2 + 3x - 3 = 0
∆ ’ = 3 2 -4.1.(-3 )=9 +12=21 > 0
∆ ' = 21
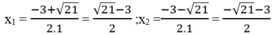
Với m = -4 ta có: x 2 +3x -1 = -4 ⇔ x 2 +3x +3 = 0
∆ = 3 2 -4.1.3=9 -12 = -3 < 0
Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
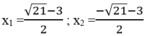
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:
7
x
-
y
+
2
-
5
x
+
y
-...
Đọc tiếp
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ: 7 x - y + 2 - 5 x + y - 1 = 4 , 5 3 x - y + 2 + 2 x + y - 1 = 4
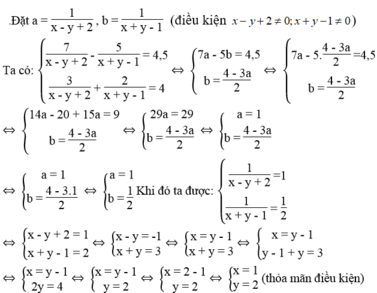
Vậy nghiệm của hệ phương trình là (x; y) = (1; 2).
Đúng 0
Bình luận (0)
Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: 2 + 2 x 2 - 1 = 2 x 2 - 2
Hướng dẫn: Đặt u = x 2 - 1.
Nếu đặt u = x 2 − 1 thì x 2 = u + 1 nên phương trình có dạng
( 2 + 2)u = 2(u + 1) − 2 (1)
Ta giải phương trình (1):
(1) ⇔ 2 u + 2u = 2u + 2 − 2
⇔ 2 u = 2 − 2
⇔ 2 u = 2 ( 2 − 1) ⇔ u = 2 − 1
⇔ x 2 − 1 = 2 − 1
⇔ x 2 = 2
⇔ x = 1
Đúng 0
Bình luận (0)
Giải phương trình sau bằng cách đặt ẩn phụ:
\(\dfrac{x}{\sqrt{4x-1}}+\dfrac{\sqrt{4x-1}}{x}=2\)
Đặt \(\dfrac{x}{\sqrt{4x-1}}=a\)
Theo đề, ta có phương trình:
a+1/a=2
\(\Leftrightarrow a+\dfrac{1}{a}=2\)
\(\Leftrightarrow\dfrac{a^2+1-2a}{a}=0\)
=>a=1
=>\(x=\sqrt{4x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=4x-1\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=3\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow x\in\left\{2+\sqrt{3};2-\sqrt{3}\right\}\)
Đúng 3
Bình luận (0)
Giải các phương trình sau bằng cách đặt ẩn số phụ
2
x
2
x
+
1
2
-
5
x
x...
Đọc tiếp
Giải các phương trình sau bằng cách đặt ẩn số phụ 2 x 2 x + 1 2 - 5 x x + 1 + 3 = 0
Đặt m = x/(x+1) .Điều kiện : x ≠ -1
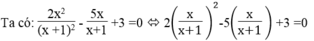
⇔ 2 m 2 -5m +3 =0
Phương trình 2m2 -5m +3 = 0 có hệ số a = 2, b = -5 , c = 3 nên có dạng
a +b + c = 0
suy ra : m 1 = 1 , m 2 =3/2
Với m 1 =1 ta có: x/(x+1) =1 ⇔ x =x+1 ⇔ 0x =1 (vô nghiệm)
Với m = 3/2 ta có: x/(x+1) = 3/2 ⇔ 2x =3(x +1)
⇔ 2x =3x +3 ⇔ x =-3
Giá trị của x thỏa mãn điều kiện bài toán
Vậy phương trình đã cho có 1 nghiệm : x=-3
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:
1
x
+
1
y
4
5
1
x...
Đọc tiếp
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ: 1 x + 1 y = 4 5 1 x - 1 y = 1 5
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:
15
x
-
7
y
9
4
x
+
9
y...
Đọc tiếp
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ: 15 x - 7 y = 9 4 x + 9 y = 35







