Tính giá trị biểu thức sau: B = 3 - sin2900 + 2cos2600 - 3tan2450
A. -1
B. 0
C. - 1 2
D. 2
1, Giá trị của biểu thức: \(x^3\) + 3\(x^2\) + 3x tại x = 9 là:
A. 999. B. 1001. C. 99. D. 101.
2, Tính giá trị của biểu thức A = \(x^2\)- \(y^2\) + 2y - 1 với x = 3 và y = 1.
A. -9. B. 0. C. 9. D. -1.
Tính giá trị biểu thức A = sin 2 1 0 + sin 2 2 0 + … + sin 2 88 0 + sin 2 89 0 + sin 2 90 0
A. A = 46
B. A = 93 2
C. A = 91 2
D. A = 45
Ta có:
![]()
![]()
Nên A = ( sin 2 1 0 + sin 2 89 0 ) + ( sin 2 2 0 + sin 2 88 0 ) +… + ( sin 2 44 0 + sin 2 46 0 ) + sin 2 45 0 + sin 2 90 0
= ( sin 2 1 0 + c o s 2 1 0 ) + ( sin 2 2 0 + c o s 2 2 0 ) + … + ( sin 2 44 0 + c o s 2 44 0 ) + sin 2 45 0 + sin 2 45 0
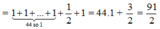
Vậy A = 91 2
Đáp án cần chọn là: C
1.Biết a-2b=5, hãy tính giá trị của biểu thức :P=(3a-2b)/(2a+5)+(3b-a)/(b-5)
2.Cho a+b+c=0.Tính giá trị của các biểu thức sau:
A=1/(a^2+b^2-c^2)+1/(b^2+c^2-a^2)+1/(c^2+a^2-b^2)
P=3a-2b\2a+5 + 3b-a\b-5
=2a+a-2b\2a-5 + -a+2b+b\b-5
=2a+(a-2b)\2a-5 + -(a-2b)+b
=2a+5\2a-5 + -5+b\b-5
=-(2a-5)\(2a-5) + (b-5)\(b-5)
=-1+1=0
Bài 2: Thu gọn và tìm bậc của các đơn thức sau a) 2 5xy 2bx y ; b) 4 2 4 ab c 20a bx 5 ; c) 2 2 1 1,5xy bcx b 4 ; d) 2 3 2 2 1 2ax y x y zb 2 Bài 3: Cho biểu thức A = 2 3 𝑥 3 . 3 4 𝑥𝑦 2 . 𝑧 2 và B = 9x𝑦 3 . (−2𝑥 2𝑦𝑧 3 ) 1) Thu gọn và tìm bậc của đơn thức thu gọn A và B 2) Cho biết phần biến và phần hệ số của đơn thức thu gọn A và B 3) Tính tích của hai đơn thức thu gọn A và B. Bài 4:Cho đơn thức C = 2𝑥𝑦 2 ( 1 2 𝑥 2𝑦 2𝑥) ; D = 2 3 𝑥𝑦 2 . ( 3 2 𝑥) a) Thu gọn đơn thức C, D. Xác định phần hệ sô, phần biến, tìm bậc của đơn thức. b) Tính giá trị của đơn thức C tại x= 1, y = -1 c) Tính giá trị của đơn thức D tại x = -1, y = -2 d) Chứng minh đơn thức C,D luôn nhận giá trị dương với mọi x ≠ 0, y ≠ 0, Bài 5. Cho A = 3xy – 4xy + 10xy – xy a) Tính giá trị của A tại x = 1, y = -1 b) Tìm điều kiện của x, y để A > 0. c) Tìm điều kiện của x, y để A > 0. d) Tìm x, y nguyên để A = - 24
Bài 2: Thu gọn và tìm bậc của các đơn thức sau a) 2 5xy 2bx y ; b) 4 2 4 ab c 20a bx 5 ; c) 2 2 1 1,5xy bcx b 4 ; d) 2 3 2 2 1 2ax y x y zb 2 Bài 3: Cho biểu thức A = 2 3 𝑥 3 . 3 4 𝑥𝑦 2 . 𝑧 2 và B = 9x𝑦 3 . (−2𝑥 2𝑦𝑧 3 ) 1) Thu gọn và tìm bậc của đơn thức thu gọn A và B 2) Cho biết phần biến và phần hệ số của đơn thức thu gọn A và B 3) Tính tích của hai đơn thức thu gọn A và B. Bài 4:Cho đơn thức C = 2𝑥𝑦 2 ( 1 2 𝑥 2𝑦 2𝑥) ; D = 2 3 𝑥𝑦 2 . ( 3 2 𝑥) a) Thu gọn đơn thức C, D. Xác định phần hệ sô, phần biến, tìm bậc của đơn thức. b) Tính giá trị của đơn thức C tại x= 1, y = -1 c) Tính giá trị của đơn thức D tại x = -1, y = -2 d) Chứng minh đơn thức C,D luôn nhận giá trị dương với mọi x ≠ 0, y ≠ 0, Bài 5. Cho A = 3xy – 4xy + 10xy – xy a) Tính giá trị của A tại x = 1, y = -1 b) Tìm điều kiện của x, y để A > 0. c) Tìm điều kiện của x, y để A > 0. d) Tìm x, y nguyên để A = - 24
1) cho A=x/x-1 + x/x+1 (x ko bằng +-1) và B=X^2-x/x^2-1 (x ko bằng +-1)
a)rút gọn A và tính A khi x=2
b)Rút gọn B và tìm x để B=2/5
c)tìm x thuộc Z để (A,B)thuộc Z
2)A =(2+x/2-x - 4x^2/x^2-4 - 2-x/2+x) : x^2 - 3x/2x^2 - x^3
a)rút gọn biểu thức A b) tính giá trị biểu thức A khi /x-5/=2
c)tìm x để A>0
3)B= x+2/x+3 - 5/x^2+x-6 - 1/2-x
a)rút gọn biểu thức B b)tìm x để B=3/2 c) tìm giá trị nguyên của x để B có giả trị nguyên
4)C= (2x/2x^2-5x+3 - 5/2x-3) : (3+2/1-x)
a)rút gọn biểu thức C b) tìm giá trị nguyên của biểu thức C biết :/2x-1/=3
c)tìm x để B >1 d) tìm giá trị nhỏ nhất của biểu thức C
5)D=(1 + x/x^2+1) : (1/x-1 - 2x/x^3+x-x^2-1)
a)rút gọn biểu thức D
b)tìm giá trị của x sao cho D<1
c)tìm giá trị nguyên của x để B có giá trị nguyên
bạn viết thế này khó nhìn quá
nhìn hơi đau mắt nhá bạn hoa mắt quá
1. Chứng minh rằng các biểu thức sau luôn có giá trị âm với mọi giá trị của biến: a) -9*x^2 + 12*x -15 b) -5 – (x-1)*(x+2)
2. Chứng minh các biểu thức sau luôn có giá trị dương với mọi giá trị của biến: a) x^4 +x^2 +2 b) (x+3)*(x-11) + 2003
3. Tính a^4 +b^4 + c^4 biết a+b+c =0 và a^2 +b^2 +c^2 = 2
Bài 1) Chứng minh rằng các biểu thức sau luôn có giá trị âm với mọi giá trị của biến:
a) 9x^2+12x-15
=-(9x^2-12x+4+11)
=-[(3x-2)^2+11]
=-(3x-2)^2 - 11.
Vì (3x-2)^2 không âm với mọi x suy ra -(3x-2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x
Do đó -[(3*x)-2]^2-11 < 0 với mọi giá trị của x.
Hay -9*x^2 + 12*x -15 < 0 với mọi giá trị của x.
b) -5 – (x-1)*(x+2)
= -5-(x^2+x-2)
=-5- (x^2+2x.1/2 +1/4 - 1/4-2)
=-5-[(x-1/2)^2 -9/4]
=-5-(x-1/2)^2 +9/4
=-11/4 - (x-1/2)^2
Vì (x-1/2)^2 không âm với mọi x suy ra -(x-1/2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x
Do đó -11/4 - (x-1/2)^2 < 0 với mọi giá trị của x.
Hay -5 – (x-1)*(x+2) < 0 với mọi giá trị của x.
Bài 2)
a) x^4+x^2+2
Vì x^4 +x^2 lớn hơn hoặc bằng 0 vơi mọi x
suy ra x^4+x^2+2 >=2
Hay x^4+x^2+2 luôn dương với mọi x.
b) (x+3)*(x-11) + 2003
= x^2-8x-33 +2003
=x^2-8x+16b + 1954
=(x-4)^2 + 1954 >=1954
Vậy biểu thức luôn có giá trị dương với mọi giá trị của biến
1/ \(-9x^2+12x-15=\left(-9x^2+2.2.3x-4\right)-11\)
\(=-11-\left(3x-2\right)^2\le-11< 0\)
Câu b và câu 2 tương tự
Bài 1: Tính giá trị các biểu thức sau tại: |x| = \(\dfrac {1}{3}\); |y| = 1
a) A= 2x2 - 3x + 5 b) B= 2x2 - 3xy + y2
Bài 2: Tính giá trị các biểu thức A sau biết x + y +1 = 0:
A= x (x + y) - y2 (x + y) + x2 - y2 + 2 (x + y) + 3
Bài 3: Cho x.y.z = 2 và x + y + z = 0. Tính giá trị biểu thức:
A= (x + y)(y + z)(z + x)
Bài 4: Tìm các giá trị của các biến để các biểu thức sau có giá trị bằng 0:
a) |2x - \(\dfrac {1}{3}\)| - \(\dfrac {1}{3}\) b) |2x - \(\dfrac {1}{3}
\)| - \(\dfrac {1}{3}\) c) |3x + 2\(\dfrac {1}{3}
\)| + |y + 2| = 0 d) (x - 2)2 + (2x - y + 1)2 = 0
Bài 1:
|\(x\)| = 1 ⇒ \(x\) \(\in\) {-\(\dfrac{1}{3}\); \(\dfrac{1}{3}\)}
A(-1) = 2(-\(\dfrac{1}{3}\))2 - 3.(-\(\dfrac{1}{3}\)) + 5
A(-1) = \(\dfrac{2}{9}\) + 1 + 5
A (-1) = \(\dfrac{56}{9}\)
A(1) = 2.(\(\dfrac{1}{3}\) )2- \(\dfrac{1}{3}\).3 + 5
A(1) = \(\dfrac{2}{9}\) - 1 + 5
A(1) = \(\dfrac{38}{9}\)
|y| = 1 ⇒ y \(\in\) {-1; 1}
⇒ (\(x;y\)) = (-\(\dfrac{1}{3}\); -1); (-\(\dfrac{1}{3}\); 1); (\(\dfrac{1}{3};-1\)); (\(\dfrac{1}{3};1\))
B(-\(\dfrac{1}{3}\);-1) = 2.(-\(\dfrac{1}{3}\))2 - 3.(-\(\dfrac{1}{3}\)).(-1) + (-1)2
B(-\(\dfrac{1}{3}\); -1) = \(\dfrac{2}{9}\) - 1 + 1
B(-\(\dfrac{1}{3}\); -1) = \(\dfrac{2}{9}\)
B(-\(\dfrac{1}{3}\); 1) = 2.(-\(\dfrac{1}{3}\))2 - 3.(-\(\dfrac{1}{3}\)).1 + 12
B(-\(\dfrac{1}{3};1\)) = \(\dfrac{2}{9}\) + 1 + 1
B(-\(\dfrac{1}{3}\); 1) = \(\dfrac{20}{9}\)
B(\(\dfrac{1}{3};-1\)) = 2.(\(\dfrac{1}{3}\))2 - 3.(\(\dfrac{1}{3}\)).(-1) + (-1)2
B(\(\dfrac{1}{3}\); -1) = \(\dfrac{2}{9}\) + 1 + 1
B(\(\dfrac{1}{3}\); -1) = \(\dfrac{20}{9}\)
B(\(\dfrac{1}{3}\); 1) = 2.(\(\dfrac{1}{3}\))2 - 3.(\(\dfrac{1}{3}\)).1 + (1)2
B(\(\dfrac{1}{3}\); 1) = \(\dfrac{2}{9}\) - 1 + 1
B(\(\dfrac{1}{3}\);1) = \(\dfrac{2}{9}\)
Bài 2:
\(x+y+1=0\Rightarrow x+y=-1\)
A = \(x\)(\(x+y\)) - y2.(\(x+y\)) + \(x^2\) - y2 + 2(\(x+y\)) + 3
Thay \(x\) + y = -1 vào biểu thức A ta có:
A = \(x\).( -1) - y2 .(-1) + \(x^2\) - y2 + 2(-1) + 3
A = -\(x\) + y2 + \(x^2\) - y2 - 2 + 3
A = \(x^2\) - \(x\) + 1
Cho 2 biểu thức
A=(√x / √x-1 - 1/x-√x) : √x+1 / √x+2
B=√x /√x-3
x>0 ; x khác 1;x khác 9
a) tính giá trị biểu thức B khi x=36
b) tìm x để B<1/2
c) rút gọn A
d) tin giá trị x nguyên nhỏ nhất để P=A. B nguyên