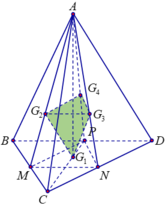
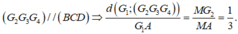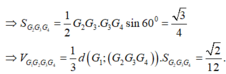Cho tứ diện ABCD và điểm G thỏa mãn G A ⇀ + G B ⇀ + G C ⇀ + G D ⇀ = 0 ⇀ (G gọi là trọng tâm của tứ diện). Gọi G A = G A ∩ ( B C D ) . Trong các khẳng định sau, khẳng định nào đúng?
A. G A ⇀ = - 3 G A G ⇀
B. G A ⇀ = 4 G A G ⇀
C. G A ⇀ = 3 G A G ⇀
D. G A ⇀ = 2 G A G ⇀
Đáp án C.
+ Gọi G 0 là trọng tâm tam giác BCD=> G B ⇀ + G C ⇀ + G D ⇀ = 3 G G 0 ⇀
=>
G
A
⇀
+
G
B
⇀
+
G
C
⇀
+
G
D
⇀
=
0
⇀
=> A, G, G 0 thẳng hàng ⇒ G 0 = G A
+ Có A, G,
G
A
thẳng hàng mà 
Cho tứ diện ABCD. trên cạnh AB lấy điểm M thỏa mãn AM=$\frac{1}{4}$ AB, G là trọng tâm tam giác BCD. Tìm:
a. Giao điểm của GD và (ABC);
b. Giao điểm của MG với (ACD).
Trong (BCD): DG BC = F
Vậy DG (ABC) = F.
b. Cách 1: MG (BMG) (ABH) (H = BG DC)
(Do mặt phẳng (BMG) "lơ lửng" trong hình chóp nên ta kéo dài BM thành BA và BG thành BH để ta có cái nhìn dễ dàng hơn đối với mặt phẳng này).
(BMG) (ACD) =AH
Trong (ABH): MG AH =K
Vậy MG (ACD) = K.
a. Trong (BCD) có GD và BC cắt nhau tại K
vậy K = GD và (ABC)
b. có MG ⊂ (BMG) trùng (ABH) có H = BG và DC
(BMG) và (ACD) = AH
Trong (ABH) có MG và AH = P
Vậy MG và (ACD) = P
a, Trong (BCD): DG cắt BC = F
Vậy DG cắt (ABC) = F
b,MG nằm trong (DMF).
Trong (ABC) AC cắt MF = H
Vậy (DMF) cắt (ABC) = DH
Trong (DMF): MG cắt DH = K
Vậy MG cắt (ABC) = K
Cho tứ diện ABCD. Trên cạnh AB lấy điểm M thỏa mãn AM= $\frac{1}{4}$ AB, G là trọng tâm tam giác BCD. Tìm:
a. Giao điểm của GD với (ABC).
b. Giao điểm của MG với (ACD).
Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Chứng minh ba điểm I, G, J thẳng hàng.
Ta có:
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {GI} + \overrightarrow {IA} } \right) + \left( {\overrightarrow {GI} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JC} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {GI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) + 2\overrightarrow {GJ} + \left( {\overrightarrow {JC} + \overrightarrow {JD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \Leftrightarrow 2\left( {\overrightarrow {GI} + \overrightarrow {GJ} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \Rightarrow \)G là trung điểm của đoạn thẳng IJ
Vậy I, G, J thẳng hàng
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp
A. GM = GN
B. G M → + G N → = 0 →
C. G A → + G B → + G C → + G D → = 0
D. P G → = 1 / 4 ( P A → + P B → + P C → + P D → ) , với P là điểm bất kì.
Điều kiện GM = GN mới chứng tỏ điểm G nằm trên mặt phẳng trung trực của đoạn thẳng MN.
Đáp án A
Cho tứ diện ABCD. M,N lần lượt là trung điểm của AD và BD; G là trọng tâm tam giác ABC.
a) Tìm giao tuyến của mặt phẳng (ABC) và (MNG);
b) Xác định thiết diện tạo bởi (MNG) và tứ diện ABCD.
G là điểm chung của hai mặt phẳng (ABC) và (MNG).
Ta có BC // MN (Do MN là đường trung bình của tam giác ABD).
Vậy giao tuyến của hai mặt phẳng (ABC) và (MNG) là đường thẳng d đi qua G song song với BC.
Trong (ABC): d BC = P
d AC = QVậy thiết diện cần tìm là tứ giác MNPQ.
a) G là điểm chung của hai mặt phẳng (ABC) và (MNG)
Ta có BC // MN (Do MN là đường trung bình của tam giác ABD).
Vậy giao tuyến của hai mặt phẳng (ABC) và (MNG) là đường thẳng d đi qua G // BC.
b) Trong (ABC): d BC = P
d ∩ AC =Q
Vậy thiết diện cần tìm là tứ giác MNPQ
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G₁, G₂, G₃, G₄ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G₁G₂G₃G₄.
A. 2 4
B. 2 18
C. 9 2 32
D. 2 12
Chọn D
Tứ diện đều ABCD ⇒ A G 1 ⊥ B C D
Ta có ngay 
Cạnh C G 1 = B C 3 = 3 ⇒ G 1 A = A C 2 - G 1 C 2 = 6 ⇒ d G 1 ; G 2 G 3 G 4 = 6 3
Lại có G 2 G 3 M N = A G 2 A M = 2 3 ⇒ G 2 G 3 = 2 3 M N = 1 3 B D = 1
Tương tự G₃G₄=1, G₄G₂=1 ⇒ ∆ G 2 G 3 G 3 là tam giác đều có cạnh bằng 1
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
A. G A → + G B → + G C → + G D → = 0 →
B. 4 P G → = P A → + P B → + P C → + P D → với P là điểm bất kỳ
C. G M = G N
D. G M → + G N → = 0 →
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
với P là điểm bất kỳ
