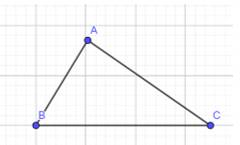
a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.

\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)

b) 

Theo định lí tổng 3 góc trong tam giác ABC, ta có:

\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)

 \( \Rightarrow\widehat C = \widehat B = {40^o}\)

\( \Rightarrow \) ABC là tam giác cân tại A.

Câu hỏi của Duy Đinh Tiến - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo link này nhé!

A nhó

A. góc A bằng 40*; góc B bằng 60*; góc C bằng 80*

Câu A

Áp dụng định lí sin trong tam giác ABC ta có:

 \(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)

\( \Rightarrow R = \dfrac{a}{{2\sin A}};\;\;b = \dfrac{{a.\sin B}}{{\sin A}}\)

Mà \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\)

\( \Rightarrow R = \dfrac{{10}}{{2\sin {{45}^o}}} = 5\sqrt 2 ;\;\;b = \dfrac{{a.\sin {{70}^o}}}{{\sin {{45}^o}}} \approx 13,29\)

Mặt khác: \(\widehat A = {45^o},\widehat B = {70^o} \Rightarrow \widehat C = {65^o}\)

Từ định lí sin ta suy ra: \(c = \dfrac{{a.\sin C}}{{\sin A}} = \dfrac{{10.\sin {{65}^o}}}{{\sin {{45}^o}}} \approx 12,82.\)

Vậy \(R = 5\sqrt 2 ;\;\;b \approx 13,29\); \(c \approx 12,82.\)

 a)

Theo tính chất đường phân giác áp dụng cho \(\Delta ABC\) có BD là phân giác góc ABC \(\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{1}{2}\)

\(\Delta ABC\) vuông tại A\(\Rightarrow\tan B=\frac{AB}{BC}=\frac{1}{2}\Rightarrow\widehat{B}\approx27\)

b, 

Thấy \(\widehat{ACB}\) nội tiếp \(\left(O\right)\) chắn cung AB nhỏ 

\(\Rightarrow\widehat{ACB}=\frac{1}{2}sđ\overline{AB}\left(1\right)\)

Thấy \(\widehat{AOB}\) chắn cung AB nhỏ \(\Rightarrow\widehat{AOB}=sđ\overline{AB}\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\widehat{AOB}=2\widehat{ACB}=2\left(180^o-70^o-60^o\right)=2.50^o=100^o\)

Bài 1:

Xét \(\Delta ABC\) có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(ĐL tổng 3 góc 1 \(\Delta\))

\(\Rightarrow30^o+70^o+\widehat{C}=180^o\) (Vì \(\widehat{A}=30^o;\widehat{B}=70^o\) (gt))

\(\Rightarrow\widehat{C}=180^o-30^o-70^o=80^o\)

Bài 2:

Xét \(\Delta ABC\) (vuông tại A) có:

\(\widehat{B}+\widehat{C}=90^o\) (Tc \(\Delta\) vuông)

\(\Rightarrow\widehat{B}+40^o=90^o\) (Vì \(\widehat{C}=40^o\) (gt))

\(\Rightarrow\widehat{B}=90^o-40^o=50^o\)

Giải:

+) Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) ( 3 góc của tam giác )

\(\Rightarrow30^o+70^o+\widehat{C}=180^o\)

\(\Rightarrow\widehat{C}=80^o\)

Vậy...

+) Ta có: \(\widehat{B}+\widehat{C}=90^o\) ( do tam giác có \(\widehat{A}=90^o\) )

\(\Rightarrow40^o+\widehat{B}=90^o\)

\(\Rightarrow\widehat{B}=50^o\)

Vậy...

hjuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu

To moi hoc lop 

helppppppppppppp