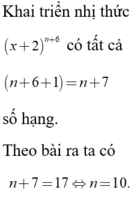xời dăm ba cái bài này tui...........................ko thik làm 

+ Ta có: \(6n⋮6\forall n\)\(\Rightarrow\)\(6n+3:6\)dư  \(3\)

                                            \(6n-3:6\)dư  \(6-3=3\)

+ Ta lại có: \(6.\left(n+3\right)⋮6\forall n\)\(\Rightarrow\)\(6.\left(n+3\right)+3:6\)dư  \(3\)

Vậy \(6n+3,\)\(6n-3,\)\(6.\left(n+3\right)+3\)chia 6 dư 3

6.n + 3               (với n ∈ ℕ)  ( vì \(6n⋮6\), 3 không chia hết cho 6 )

6.n - 3                (với n ∈ ℕ )   (  vì \(6n⋮6\), 3 không chia hết cho 6  )

6.(n + 3) + 3       (với n ∈ ℕ)  ( vì \(6\left(n+3\right)⋮6\), 3 không chia hết cho 6 )

\(\rightarrow\)Chia 6 dư 3

Chồi ôi Thu lấy đề của ai nhỉ

Xuân Tuấn Trịnh29 tháng 4 2017 lúc 9:10

a) Để A là phân số thì 5 không chia hết cho n-1 hay n-1 không phải Ư(5) mà Ư(5)={-5;-1;1;5}

Ta có bảng sau:

Vậy n≠{−4;0;2;6}≠{−4;0;2;6}thì A là phân số

n=0 => A=50−1=−550−1=−5

n=10 => A=510−1=59510−1=59

n=-2 => A=5−2−1=−535−2−1=−53

Để A là số nguyên =>5 chia hết cho n-1 <=>n-1 là Ư(5)

Từ bảng trên => n={-4;0;2;6} thì A nguyên

b) Do n là Số tự nhiên => n và n+1 là 2 số tự nhiên liên tiếp

=>n và n+1 nguyên tố cùng nhau

=>phân số nn+1nn+1tối giản(dpcm)

c)11⋅2+12⋅3+...+149⋅50=1−12+12−13+...+149−150=1−150<1(đpcm)

~hok tốt~

Vì \(n+2⋮n-1\)

\(\Rightarrow\left(n-1\right)+3⋮n-1\)

mà \(n-1⋮n-1\Rightarrow3⋮n-1\)

\(\Rightarrow n-1\inƯ\left(3\right)\)

\(\Rightarrow n-1\in\left\{\pm1;\pm3\right\}\)

\(\Rightarrow n\in\left\{2;0;4;-2\right\}\)

Vậy \(n\in\left\{0;\pm2;4\right\}.\)

Để \(\dfrac{n+2}{n-1}\) nhận giá trị nguyên thì :

\(n+2\text{ }⋮\text{ }n-1\)

\(\Rightarrow n-\left(1+3\right)\text{ }⋮\text{ }n-1\)

\(\Rightarrow n-1+3\text{ }⋮\text{ }n-1\)

\(\Rightarrow\left(n-1\right)+3\text{ }⋮\text{ }n-1\)

Mà \(n-1\text{ }⋮\text{ }n-1\)

\(\Rightarrow3\text{ }⋮\text{ }n-1\)

\(\Rightarrow\left(n-1\right)\inƯ_{\left(3\right)}\)

\(\Rightarrow\left(n-1\right)\in\left\{-1;1;-3;3\right\}\)

\(\Rightarrow n\in\left\{0;2;-2;4\right\}\)

Vậy \(\dfrac{n+2}{n-1}\) nhận giá trị nguyên khi \(n\in\left\{0;2;-2;4\right\}\)

\(\dfrac{A}{B}=\dfrac{3}{2}x^{n-4}y^2-\dfrac{5}{2}x^{n-4}\)

Để A chia hết cho B thì n-4>=0

hay n>=4

ai nhanh mk k

\(n+6⋮n+2\)

\(\Leftrightarrow n+2+4⋮n+2\)

Mà \(n+2⋮n+2\)

\(\Rightarrow4⋮n+2\)

\(\Rightarrow n+2\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)

\(\Rightarrow n\in\left\{-1;-3;0;-4;2;-6\right\}\)

\(n+6⋮n+2\)

\(\Rightarrow n+2+4⋮n+2\)

Vì \(n+2⋮n+2\)

\(\Rightarrow4⋮n+2\)

    \(n+2\inƯ\left(4\right)=\left\{1;2;4\right\}\)

  \(\Rightarrow n\in\left\{0;2\right\}\)

         Vậy ................

Xét các trường hợp:

\(n=1\Leftrightarrow1!=1=1^2\) là số chính phương 

\(n=2\Leftrightarrow1!+2!=3\) không phải là số chính phương

\(n=3\Leftrightarrow1!+2!+3!=9=3^3\) là số chính phương 

\(n\ge4\Leftrightarrow1!+2!+3!+4!=33\) còn \(5!,6!,7!,...,n!\) đều có tận cùng là \(0\Rightarrow1!+2!+3!+...+n!\) có tận cùng là chữ số 3 nên không phải là số chính phương

Vậy \(n\in\left\{1;3\right\}\).

Đáp án C.

Chọn C

Khai triển  ( x + 2 ) n + 5 ,   ( n ∈ ℕ )  có tất cả 2019 số hạng nên (n+5) + 1 = 2019 => n = 2013