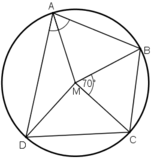
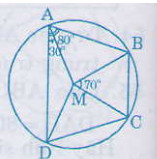
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết:
DAB → = 80 ° ; DAM → = 30 ° ; BMC → = 70 °
Hãy tính số đo góc
MAB ^ , BCM → , AMB → , DMC AMD → , MCD → , BCD →
Những câu hỏi liên quan
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết:
D
A
B
^
80
o
;
D
A
M
^
30
o
;
B
M
C
^
70
o...
Đọc tiếp
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết:
D A B ^ = 80 o ; D A M ^ = 30 o ; B M C ^ = 70 o . Hãy tính số đo các góc
M A B ^ , B C M ^ , A M B ^ , D M C ^ , A M D ^ , M C D ^ , B C D ^
Ta có:
(1)
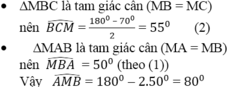(3)
(số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
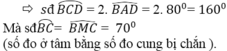
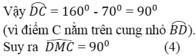
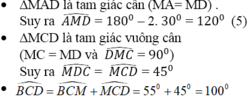
(theo (2) và (6) và Cm là tia nằm giữa hai tia CB,CD).
Đúng 0
Bình luận (0)
cho tứ giác ABCD nội tiếp đường tròn. gọi r1,r2,r3,r4 lần lượt là tâm đường tròn nội tiếp các tam giác BCD,CDA,DAB,ABC
chứng minh rằng r1+r3=r2+r4
Cho tứ giác ABCD nội tiếp đường tròn O. Gọi E,F,G,H lần lượt là tâm đường tròn nội tiếp của các tam giác ABC, BCD, CDA, DAB. CMR: EFGH là hình chữ nhật.
C1a) cho đường tròn tâm O góc nội tiếp BCD60 độ kẻ đường kính CA tính số đo góc ACBb) tứ giác ABCD nội tiếp đường tròn có góc DAB120 độ số đo góc BCD bằng bao nhiêuC2 cho đường tròn tâm O và điểm M nằm ngoài đường tròn từ M kẻ 2 tiếp tuyến MA ,MB đến đg tròn tâm O với A,B là các tiếp điểm qua M kẻ các tiếp tuyến MNP (ML nhỏ hơn MP) đến đường tròn tâm O .gọi K là trung điểm của NP,OM cắt AB tại Ha) chứng minh rằng MAKOB cùng thuộc một đường trònb) chứng minh KM là phân giác của góc AKBGIÚP EM VỚI...
Đọc tiếp
C1
a) cho đường tròn tâm O góc nội tiếp BCD=60 độ kẻ đường kính CA tính số đo góc ACB
b) tứ giác ABCD nội tiếp đường tròn có góc DAB=120 độ số đo góc BCD bằng bao nhiêu
C2 cho đường tròn tâm O và điểm M nằm ngoài đường tròn từ M kẻ 2 tiếp tuyến MA ,MB đến đg tròn tâm O với A,B là các tiếp điểm qua M kẻ các tiếp tuyến MNP (ML nhỏ hơn MP) đến đường tròn tâm O .gọi K là trung điểm của NP,OM cắt AB tại H
a) chứng minh rằng MAKOB cùng thuộc một đường tròn
b) chứng minh KM là phân giác của góc AKB
GIÚP EM VỚI MAI THI GIỮA KÌ HUHU
2:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: ΔONP cân tại O
mà OK là trung tuyến
nên OK vuông góc NP
góc OKM=góc OAM=góc OBM=90 độ
=>O,P,A,M,B cùng nằm trên đường tròn đường kính OM
góc AKM=góc AOM
góc BKM=góc BOM
mà góc AOM=góc BOM
nên góc AKM=góc BKM
=>KM là phân giác của góc AKB
Đúng 1
Bình luận (0)
cho tứ giác ABCD nội tiếp : O1;O2;O3;O4 lần lượt là tâm đường tròn nôi tiếp các tam giác ABC,BCD,CDA,DAB,chứng minh rằng O1O2O3O4 là hình chữ nhật
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết \(\widehat{DAB}=80^o,\widehat{DAM}=30^o;\widehat{BMC}=70^o.\)
Hãy tính số đo các góc \(\widehat{MAB};\widehat{BCM};\widehat{AMB};\widehat{DMC};\widehat{AMD};\widehat{MCD}\) và \(\widehat{BCD}.\)
Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD
Đúng 1
Bình luận (0)
Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R, đường kính BC. Lấy điểm A trên tia đối của CB. Kẻ tiếp tuyến AF của nữa đường tròn O với F là tiếp điểm. Tia AF cắt tiếp tuyến Bx của nữa đường tròn. Biết AF 48/3a. Chứng minh BODF là tứ giác nội tiếp,tìm tâm đường tròn ngoại tiếp tứ giácb. Tính cos góc DABc. Cho OM vuông góc BC (M thuộc AD) chứng minh BD/DM - DM / AM 1d. Tính diện tích tứ giác OBDM ở ngoài đường tròn theo R
Đọc tiếp
Cho đường tròn tâm O bán kính R, đường kính BC. Lấy điểm A trên tia đối của CB. Kẻ tiếp tuyến AF của nữa đường tròn O với F là tiếp điểm. Tia AF cắt tiếp tuyến Bx của nữa đường tròn. Biết AF = 48/3
a. Chứng minh BODF là tứ giác nội tiếp,tìm tâm đường tròn ngoại tiếp tứ giác
b. Tính cos góc DAB
c. Cho OM vuông góc BC (M thuộc AD) chứng minh BD/DM - DM / AM = 1
d. Tính diện tích tứ giác OBDM ở ngoài đường tròn theo R
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) (vói F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Cho biết AF
4
R
3
a, Chứng minh tứ giác OBDF nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác nàyb, Tính côsin góc
D
A
B...
Đọc tiếp
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) (vói F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Cho biết AF = 4 R 3
a, Chứng minh tứ giác OBDF nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác này
b, Tính côsin góc D A B ^
c, Kẻ OM ^ BC (M Î AD). Chứng minh
B
D
D
M
-
D
M
A
M
=
1
d, Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R
a, Chứng minh được DBOF nội tiếp đường tròn tâm I là trung điểm của DO
b, O A = O F 2 + A F 2 = 5 R 3 => cos D A B ^ = A F A O = 4 5
c, ∆AMO:∆ADB(g.g) => D M A M = O B O A
mà M O D ^ = O D B ^ = O D M ^ => DM = OM
=> D B D M = D B O M = A D A M . Xét vế trái B D D M - D M A M = A D - D M A M = 1
d, D B = A B . tan D A B ^ = 8 R 3 . 3 4 = 2 R => O M = A O . tan D A B ^ = 5 R 4
=> S O M D B = 13 R 2 8
S O M D B ngoài = S O M D B - 1 4 S O , R = R 2 8 13 - 2 π
Đúng 0
Bình luận (0)
cho tứ giác ABCD nt đường tròn tam O và góc DAB = 80 độ
số đo cung DAB là?
Theo tính chất góc nội tiếp, ta có:
\(\widehat{DAB}=\dfrac{1}{2}\) sđ\(\stackrel\frown{BD}\)
\(\Rightarrow\)sđ\(\stackrel\frown{BD}=2\widehat{DAB}=2.80\) độ \(=160\) độ
-Chúc bạn học tốt-
Đúng 0
Bình luận (0)