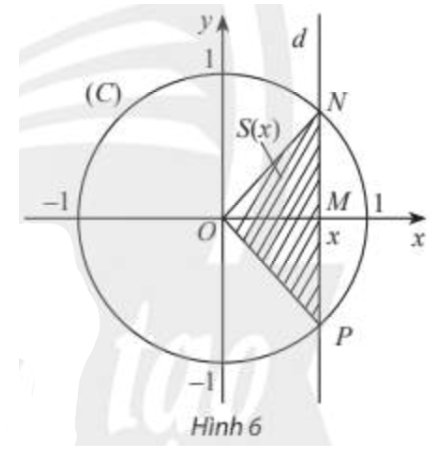
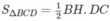Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R = 1 được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn α thì ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ∠(xOM) = α. Giả sử điểm M có tọa độ (xo; yo).
Hãy chứng tỏ rằng sinα = yo, cosα = xo, tanα = yo/xo , cotα = xo/yo .