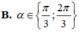
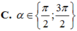
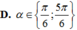
cho \(\dfrac{\pi}{2}\)<α<\(\pi\). tìm khẳng định đúng?
A. sin α<0 B. tan α>0 C. cot α>0 D. cos α<0
giải chi tiết nha
Vì 0 < α < π/2 nên sin α > 0, cos α > 0, tan α > 0, cot α > 0.
`\pi/2 < \alpha < \pi=>\alpha` nằm ở góc phần tư thứ `2`
`=>{(sin \alpha > 0;cos \alpha < 0),(tan \alpha < 0; cot \alpha < 0):}`
`->\bb D`
Cho cos α = 3/4. Hãy tìm sin α , tg α , cotg α 0 ° < α < 90 °
Cho sin α = 1/2. Hãy tìm cos α , tg α , cotg α 0 ° < α < 90 °
Cho P : x + y - z - 1 = 0 và Q : - 2 x + z + 4 = 0 và A - 1 ; 1 ; 3 . Gọi α là mặt phẳng qua A, α ⊥ P , α ⊥ Q . Tìm một vectơ pháp tuyến n → của α .
Cho điểm M(2; 1; 0) và mặt phẳng (α): x + 3y – z – 27 = 0. Tìm tọa độ điểm M' đối xứng với M qua (α).
Gọi H là hình chiếu vuông góc của M lên mp (α), ta có MH ⊥ mp (α)
Đường thẳng MH có vecto chỉ phương là n → =(1;3;-1)
x = 2 + t y = 1 + 3 t z = - t
thay x,y,z trong pt tham số của đường thẳng MH vào pt của mp (α), ta có:
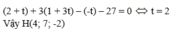
Vì M' đối xứng với M qua mp (α) nên H là trung điểm của MM'
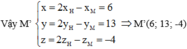
Tìm góc α ∈ π 6 ; π 4 ; π 3 ; π 2 để phương trình cos 2 x + 3 sin 2 x − 2 cos x = 0 tương đương với phương trình cos 2 x − α = cos x
A. α = π 3
B. α = π 4
C. α = π 6
D. α = π 2
Đáp án A
Ta có
cos 2 x + 3 sin 2 x − 2 cos x = 0 ⇔ sin 2 x + π 6 = cos x ⇔ cos 2 x − π 3 = cos x
Suy ra cos 2 x − π 3 = cos x ⇔ cos 2 x − α = cos x ⇔ α = π 3
Trong không gian Oxyz, cho hai mặt phẳng ( α ) : x + 2 y - z - 1 = 0 và ( β ) : 2 x + 4 y - m z - 2 = 0 . Tìm m để hai mặt phẳng α , β song song với nhau
A. m = -2
B. Không tồn tại m
C. m = 1
D. m = 2
Cho điểm M(1;4;2) và mặt phẳng α : x+y+z-1=0. Tìm khoảng cách từ điểm M đến mặt phẳng α
Cho điểm M(1;4;2) và mặt phẳng ( α ) : x + y + x - 1 = 0 . Tìm khoảng cách từ điểm M đến mặt phẳng (α).
A. 2 3
B. 2
C. 3 2
D. 3 3
Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng α : x+y-z+1=0 và β : -2x+my+2z-2=0. Tìm m để α và β song song
A. Không tồn tại m
B. m=-2
C. m=2
D. m=5
