Cho hình vẽ sau. Tam giác nào bằng với tam giác ABC
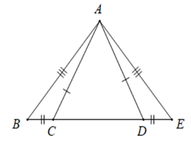
A. Δ A B C = Δ E D A
B. Δ A B C = Δ E A D
C. Δ A B C = Δ A E D
D. Δ A B C = Δ A D E
tam giác abc vuông tại a, phân giác góc b cắt ac tại d, trên cạnh bc lấy e sao cho be=ba. Chứng minh :
a, Δ ABD= Δ EBD
b, DE vuông góc với BC
c, gọi F là giao điểm của ED và AB
Chứng minh ΔABC=Δ EBD
d, CM Δ ADF=Δ EDC
e, CM FC song song với AE
giúp mk với !!!!
Xét ΔABD và ΔEBD, ta có:
AB=BE ( gt)
Góc ABD= góc EBD ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD(c-g-c)
b)Vì ΔABD=ΔEBD nên góc BAD= góc BED=90 độ( 2 cạnh tương ứng)
hay DE vuông góc với BC
c) Vì ΔABD=ΔEBD nên DA=DE ( 2 cạnh tương ứng)
Xét ΔADF và ΔEDC ta có:
góc FAD=góc CED(câu b)
AD=ED (cmt)
góc ADF=gócEDC( đối đỉnh)
⇒ΔADF=ΔEDC (g-c-g)
d,Xét ΔDAE và ΔDCF có:
DA=DC
Góc ADE=góc CDF (đối đỉnh)
DE=DF
⇒ΔDAE = ΔDCF (c-g-c)
⇒góc DAE=góc DCF (2 góc tương ứng)
MÀ 2 góc này ở vị trí SLT
⇒AE//CF
Đúg thì k
Mè sai cx k hộ nhen
Cho Δ ABC vuông tại A có góc B=300. Tia phân giác góc C cắt AB tại D. Kẻ DH vuông góc với BC (H ϵ BC).
a) C/m Δ BCD là tam giác cân và Δ ACH là tam giác đều.
b) Khi AB = 5cm. Tính BC, AC
c) Gọi I là giao điểm của HD và AC. C/m Δ IBC là tam giác đều và IC // với AH
Help mik các bạn ơi, please!
Cho Δ ABC cân tại A. Vẽ đường phân giác AE ( E thuộc BC)
a) Chứng minh Δ AEB = tam giác AEC vad AE vuông góc với BC
b) Cho biết AB = AC =5 cm và BC = 6 cm. Tính độ dài EB và AE
a: Xét ΔAEB và ΔAEC có
AE chung
góc BAE=góc CAE
AB=AC
=>ΔAEB=ΔAEC
b: EB=6/2=3cm
=>AE=4cm
Cho tam giác ABC có các đỉnh A(1;0), B(2;-3), C(-2;4) và đường thẳng Δ: x - 2y + 1 = 0. Đường thẳng Δ cắt cạnh nào của tam giác ABC?
A. AB và BC
B. AB và AC
C. AC và BC
D. Δ không cắt cạnh ΔABC
Đáp án: C
Thay lần lượt tọa độ của ba điểm A, B, C vào đường thẳng Δ ta được:
A: 1 - 2.0 + 1 = 2 > 0
B: 2 - 2.(-3) + 1 = 9 > 0
C: -2 - 2.4 + 1 = -9 < 0
Ta thấy: A và C nằm khác phía so với Δ nên Δ cắt cạnh AC
B và C nằm khác phía so với Δ nên Δ cắt cạnh BC
cho Δ ABC nhọn (AB <AC ) có ^A = 60 . D là TĐ của cạnh AC . Trên tia AB lấy điểm E / AE = AD . cm
a Δ ADE là Tam giác đều
b Δ DEC là tam giác cân
c CE ⊥ AB
Vẽ tam giác đều ABD.
Vẽ tam giác ABC vuông cân tại A (C và D nằm khác phía đối với AB).
Vẽ tam giác ADE vuông cân tại A (E và B nằm khác phía đối với AD).
a) Chứng minh: ΔACD = ΔAEB
b) Chứng minh: CD ⊥ EB
Ai đúng mình tick cho mình cần gấp
Δ Δ
a) Ta có: tam giác ABD đều => AB = AD = BD; \(\widehat{ABD}=\widehat{ADB}=\widehat{BAD}\)
tam giác ABC vuông cân tại A
=> AB = AC; góc BAC = 90o
tam giác ADE vuông cân tại A => AD = AE; góc DAE = 90o
=> AC = AE
góc BAC = góc DAE
Lại có:\(\widehat{BAC}+\widehat{BAD}=\widehat{CAD}\)
\(\widehat{DAE}+\widehat{BAD}=\widehat{EAB}\)
\(\Rightarrow\widehat{CAD}=\widehat{EAB}\)
Xét \(\Delta ACD\)và \(\Delta AEB\)có:
AC = AE (cmt)
\(\widehat{CAD}=\widehat{EAB}\)(cmt)
AD = AB (cmt)
\(\Rightarrow\Delta ACD=\Delta ABE\left(c.g.c\right)\)
Bạn giải lun cho mình câu b) ik
Cho tam giác ABC có góc A nhọn. Vẽ ra phía ngoài các tam giác ABM và ACN vuông cân tại A. BN cắt MC tại D. a) CM : Δ AMC = Δ ABN b) CM: BN ⊥⊥ CM c) Cho MB = 3cm; BC = 2cm; CN = 4cm. Tính MN. d) Chứng minh DA la tia phân giác góc MDN
a: Xét ΔABN và ΔAMC có
AB=AM
góc BAN=góc MAC
AN=AC
Do đó: ΔABN=ΔAMC
b: Gọi giao của ME với AB là D, NE với AC là F
góc AMD+góc MDA=90 độ
=>góc AMD+góc BDE=90 độ
=>góc DBE+góc BDE=90 độ
=>góc BED=90 độ
=>BN vuông góc với CM
c: BC^2+MN^2=BE^2+CE^2+ME^2+NE^2
=CN^2+BM^2
=>MN^2=7+5-3=9cm
=>MN=3cm
Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính chu vi Δ A'B'C
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ (A; AH) và đường kính HD. Qua D vẽ tiếp tuyến với đường tròn, tiếp tuyến này cắt đường thẳng BA tại điểm E. a) C/m: SinC :SinB = AB: AC
b) C/m: Δ ADE = Δ AHB.
c) C/m: CBE cân.
d, Gọi I là hình chiếu của A trên CE. C/m: CE là tiếp tuyến của đường tròn (A; AH).
a: Xét ΔABC vuông tại A có \(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}\\sinC=\dfrac{AB}{BC}\end{matrix}\right.\)
=>\(\dfrac{sinC}{sinB}=\dfrac{AB}{BC}:\dfrac{AC}{BC}=\dfrac{AB}{AC}\)
b: Xét ΔAHB vuông tại H và ΔADE vuông tại D có
AH=AD
\(\widehat{HAB}=\widehat{DAE}\)
Do đó: ΔAHB=ΔADE
c: Ta có: ΔAHB=ΔADE
=>AB=AE
=>A là trung điểm của BE
Xét ΔCEB có
CA là đường trung tuyến
CA là đường cao
Do đó: ΔCEB cân tại C
d: Ta có: ΔCEB cân tại C
mà CA là đường cao
nên CA là phân giác của góc BCE
Xét ΔCIA vuông tại I và ΔCHA vuông tại H có
CA chung
\(\widehat{ICA}=\widehat{HCA}\)
Do đó: ΔCIA=ΔCHA
=>AI=AH
Xét (A;AH) có
AI là bán kính
CE\(\perp\)AI tại I
Do đó: CE là tiếp tuyến của (A;AH)
Các bạn ơi, giúp mik bài này với!
Cho Δ ABC vuông tại A có góc B = 300. Tia phân giác góc C cắt AB tại D. Kẻ DH vuông với BC (HϵBC)
a) C/m Δ BCD là tam giác cân và Δ ACH là tam giác đều
b) Khi AB = 5cm. Tính độ dài BC, AC
c) Gọi I là giao điểm của HD và AC. C/m Δ IBC là tam giác đều và IC // với AH
(Các bạn vẽ luôn hộ mik hình nha, ko vẽ cũng đc)
Thanks các bạn nhiều!
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}=90^0-30^0=60^0\)
Ta có: CD là tia phân giác của \(\widehat{ACB}\)(gt)
nên \(\widehat{DCB}=\dfrac{\widehat{ACB}}{2}=\dfrac{60^0}{2}=30^0\)
mà \(\widehat{DBC}=30^0\)(gt)
nên \(\widehat{DBC}=\widehat{DCB}\)
Xét ΔBCD có \(\widehat{DBC}=\widehat{DCB}\)(cmt)
nên ΔBCD cân tại D(Định lí đảo của tam giác cân)
Xét ΔACD vuông tại A và ΔHCD vuông tại H có
CD chung
\(\widehat{ACD}=\widehat{HCD}\)(CD là tia phân giác của \(\widehat{ACH}\))
Do đó: ΔACD=ΔHCD(Cạnh huyền-góc nhọn)
Suy ra: CA=CH(hai cạnh tương ứng)
Xét ΔCAH có CA=CH(cmt)
nên ΔCAH cân tại C(Định nghĩa tam giác cân)
Xét ΔCHA cân tại C có \(\widehat{ACH}=60^0\)(cmt)
nên ΔCHA đều(Dấu hiệu nhận biết tam giác đều)
b) Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan\widehat{B}\)
\(\Leftrightarrow AC=5\cdot\tan30^0\)
hay \(AC=\dfrac{5\sqrt{3}}{3}cm\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+\left(\dfrac{5\sqrt{3}}{3}\right)^2=\dfrac{100}{3}\)
hay \(BC=\dfrac{10\sqrt{3}}{3}cm\)
Vậy: \(AC=\dfrac{5\sqrt{3}}{3}cm\); \(BC=\dfrac{10\sqrt{3}}{3}cm\)