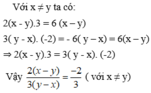a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)

\(=x^2+2x-5x-10+3x^2-12-3x+\dfrac{1}{2}x^2+5x^2\)

\(=\dfrac{19}{2}x^2-6x-22\)

Vậy biểu thức trên phụ thuộc vào biến x.

b) \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\)

Giải:

VT = \(\left(y-1\right)\left(y^2+y+1\right)\)

\(=y^3+y^2+y-y^2-y-1\)

\(=y^3-1\)

Vậy \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\).

Giải:

a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)

\(\Leftrightarrow N=x^2-3x-10+3\left(x^2-4\right)-3x+\dfrac{1}{2}x^2+5x^2\)

\(\Leftrightarrow N=x^2-3x-10+3x^2-12x-3x+\dfrac{1}{2}x^2+5x^2\)

\(\Leftrightarrow N=-10-18x+\dfrac{19}{2}x^2\)

Vậy biểu thức trên phụ thuộc vào biễn x

b) \(\left(y-1\right)\left(y^2+y+1\right)\)

\(=y^3-y^2+y^2-y+y-1\)

\(=y^3-\left(y^2-y^2\right)-\left(y-y\right)-1\)

\(=y^3-1\)

Vậy ...

\(\left(x-y\right)^3+4y\left(2x^2+y^2\right)=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)

\(\Leftrightarrow x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)

\(\Leftrightarrow\left(-3x^2y+8x^2y\right)+3xy^2+3y^3=\left(3x^2y+2x^2y\right)+3xy^2+3y^2\)

\(\Leftrightarrow5x^2y+3xy^2+3y^2=5x^2y+3xy^2+3y^2\)

\(BĐT\Leftrightarrow\left(\dfrac{x}{y+z}+1\right)+\left(\dfrac{y}{x+z}+1\right)+\left(\dfrac{z}{x+y}+1\right)\ge\dfrac{3}{2}+3=\dfrac{9}{2}\\ \Leftrightarrow\left[\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\right]\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)\ge9\left(1\right)\)

Áp dụng BĐT Cauchy:

\(\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\ge3\sqrt[3]{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)

\(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\ge3\sqrt[3]{\dfrac{1}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}}\)

Nhân vế theo vế 2 BĐT ta được

\(\left[\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\right]\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)\ge3\cdot3\sqrt[3]{1}=9\)

Do đó \(\left(1\right)\) luôn đúng

Vậy ta được đpcm

Phải có thêm dữ kiện x,y,z > 0 nữa nhé.

Áp dụng BĐT C - S dạng Engel, ta có:

Cycma(x/(y + z)) = cycma(x^2/(xy + xz)) >= cycma(x)^2/(2cycma(xy)) >= cycma(x)^2/((2cycma(x)^2)/3) = 3/2 (đpcm)

đây là BĐT Nesbit cho 3 số thực dương nên thiếu điều kiện x,y,z\(\in R\)*

a)(x-y)(x^2+xy+y^2)+xy(x-y)

=(x-y)(x^2+2xy+y^2)

=(x-y)(x+y)^2

=> Đt trên Đ

b) CM tương tự nha

\(\left(x+y\right)^2+\left(x-y\right)^2=2\left(x^2+y^2\right)\)

\(\Leftrightarrow x^2+2xy+y^2+x^2-2xy=2\left(x^2+y^2\right)\)

\(\Leftrightarrow2x^2+2y^2=2\left(x^2+y^2\right)\left(đúng\right)\)

Vậy đẳng thức đã được chứng minh

VT=(x+y)^2+(x-y)^2

=x^2+2xy+y^2+x^2-2xy+y^2

=2x^2+2y^2

=2(x^2+y^2)=VP

Vậy đẳng thức đã được chứng minh

\(VT=\dfrac{x^2+xy+2xy+2y^2}{x^2\left(x+2y\right)-y^2\left(x+2y\right)}=\dfrac{\left(x+y\right)\left(x+2y\right)}{\left(x+2y\right)\left(x-y\right)\left(x+y\right)}=\dfrac{1}{x-y}\)

BĐVT ta đc:\(\left(x+y\right)\left(x+y+z\right)-2\left(x-1\right)\left(y+1\right)+2\)

               \(=x^2+2xy+y^2+xz+yz-\left[\left(2x-1\right)\left(y+1\right)\right]\)

                   \(=x^2+2xy+y^2+xz+yz-\left(2xy+2x-y-1\right)\)

                   \(=x^2+y^2+2xy+xz+yz-2xy-2x+y+1\)

                Đề sai hả bn

mik phân tích đc như này:

x^2+xy+yx+y^2+xz+yz-(2x+2)(y+1)+2=x^2+y^2