Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Tính độ dại đường cao của hình chóp A.BCD
Những câu hỏi liên quan
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
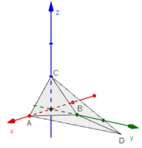
a) Cách 1:
Phương trình đoạn chắn (ABC) là:
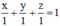hay x + y + z – 1 = 0.
Thay tọa độ điểm D(-2; 1; -1) ta được: (-2) + 1 + (-1) – 1 = -3 ≠ 0
⇒ D không nằm trong (ABC)
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của một tứ diện.
Cách 2:
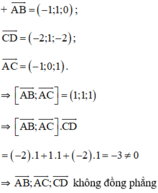
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của hình tứ diện.
Đúng 0
Bình luận (0)
Cho bốn điểm A,B,C,D. Vẽ các tam giác có đỉnh là ba trong bốn điểm đã cho. Biết rằng số tam giác vẽ được nhỏ hơn bốn. Chứng tỏ rằng trong bốn điểm đã cho ít nhất cungx có ba điểm thẳng hàng.
trang 127 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 22:07
Cho tứ diện \(ABCD\) với \(I\) và \({\rm{?}}\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\). Mệnh đề nào sau đây đúng?
A. Bốn điểm \(I,J,B,C\) đồng phẳng.
B. Bốn điểm \(I,J,A,C\) đồng phẳng.
C. Bốn điểm \(I,J,B,D\) đồng phẳng.
D. Bốn điểm \(I,J,C,D\) đồng phẳng.
Ta có:
\(\left. \begin{array}{l}J \in C{\rm{D}}\\C{\rm{D}} \subset \left( {IC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {IC{\rm{D}}} \right)\).
Vậy bốn điểm \(I,J,C,D\) đồng phẳng.
Chọn D.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm
A
1
;
-
2
;
0
,
B
1
;
0
;
-
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A 1 ; - 2 ; 0 , B 1 ; 0 ; - 1 , C 0 ; - 1 ; 2 và D 0 ; m ; p . Hệ thức giữa m và p để bốn điểm A, B, C, D đồng phẳng là
A. 2 m + p = 0
B. m + p = 1
C. m + 2 p = 3
D. 2 m - 3 p = 0
Chọn đáp án C
Ta có A B ⇀ = 0 ; 2 ; - 1 , A C ⇀ = - 1 ; 1 ; 2 và A D ⇀ = - 1 ; m + 2 ; p .
Suy ra A B ⇀ , A C ⇀ = 5 ; 1 ; 2
⇒ A B ⇀ , A C ⇀ . A D ⇀ = m + 2 p - 3
Để bốn điểm A, B, C, D đồng phẳng thì A B ⇀ , A C ⇀ . A D ⇀
⇔ m + 2 p = 3
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho bốn điểm
A
1
;
-
2
;
0
,
B
1
;
0
;
-
1
,
C
0
;
-
1
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho bốn điểm A 1 ; - 2 ; 0 , B 1 ; 0 ; - 1 , C 0 ; - 1 ; 2 và D 0 ; m ; p . Hệ thức giữa m và p để bốn điểm A, B, C, D đồng phẳng là
A. 2m + p = 0
B. m + p = 1
C. m + 2p = 3
D. 2m - 3p = 0
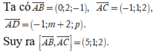
Để bốn điểm A, B, C, D đồng phẳng khi 
Chọn C.
Đúng 0
Bình luận (0)
Bài 8: Cho bốn điểm phân biệt A, B, C, D, trong đó không có ba điểm nào thẳnghàng.1) Vẽ được bao nhiêu đường thẳng đi qua hai trong số bốn điểm đã cho? Kể têncác đường thẳng đó.2) Có bao nhiêu tia trong hình đã vẽ được ở câu a)3) Có bao nhiêu tia với gốc là một trong bốn điểm đã cho và đi qua một trong cácđiểm còn lại? Kể tên các tia đó.4) Có bao nhiêu đoạn thẳng có hai mút là hai trong bốn điểm đã cho. Kể tên cácđoạn thẳng đó.
Đọc tiếp
Bài 8: Cho bốn điểm phân biệt A, B, C, D, trong đó không có ba điểm nào thẳng
hàng.
1) Vẽ được bao nhiêu đường thẳng đi qua hai trong số bốn điểm đã cho? Kể tên
các đường thẳng đó.
2) Có bao nhiêu tia trong hình đã vẽ được ở câu a)
3) Có bao nhiêu tia với gốc là một trong bốn điểm đã cho và đi qua một trong các
điểm còn lại? Kể tên các tia đó.
4) Có bao nhiêu đoạn thẳng có hai mút là hai trong bốn điểm đã cho. Kể tên các
đoạn thẳng đó.
28 tháng 6 2019 lúc 8:00
Cho tam giác ABC nhọn , các đường cao BD và CE cắt nhau tại H . Chứng minh :
a) Bốn điểm A , D, H, E cùng thuộc 1 đường tròn .
b) Bốn điểm B , E , D , C cùng thuộc 1 dường tròn.
37. a) Cho bốn điểm A,B,C,I trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng có đầu mút là hai trong bốn điểm đó. Vẽ được mấy đoạn thẳng ? Hãy kể tên các đoạn thẳng đó.
b) Cho bốn điểm A,B,C,D trong đó có ba điểm thẳng hàng. Vẽ tất cả các đoạn thẳng có đầu mút là hai trong bốn điểm đó và viết tên chúng.
a, cho bốn điểm A , B , C , D trong đó không có ba điểm nào thẳng hàng . vẽ các đoạn thẳng có đầu mút là hai trong bốn điểm đó . vẽ được mấy đoạn thẳng ? hãy kể tên các đoạn thẳng đó
b, cho bốn điểm A , B , C , D trong đó có ba điểm thẳng hàng . vẽ tất cả các đoạn thẳng có đầu mút là hai trong bốn điểm đó và cách viết tên
giúp mk nhé mk cần gấp . ai lm xong trước và chuẩn nhất mk cho
a)
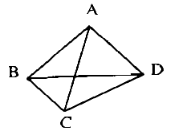
Vẽ được 6 đoạn thẳng
Tên đoạn thẳng: AB, BC, CD, AD, BD, AC
Read more: https://sachbaitap.com/cau-37-trang-130-sach-bai-tap-sbt-toan-6-tap-1-c8a5966.html#ixzz63N4AsIky
b)
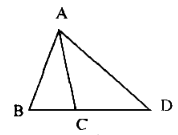
Vẽ được 6 đoạn thẳng
Tên các đoạn thẳng: AB, AD, AC, BD, BC, CD.
Read more: https://sachbaitap.com/cau-37-trang-130-sach-bai-tap-sbt-toan-6-tap-1-c8a5966.html#ixzz63N4OKsQm
a) Cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng có đầu mút là hai trong bốn điểm đó. Vẽ được mấy đoạn thẳng ? Hãy kể tên các đoạn thẳng đó ?
b) Cho bốn điểm A, B, C, D trong đó có ba điểm thẳng hàng. Vẽ tất cả các đoạn thẳng có đầu mút là hai trong bốn điểm đó và viết tên chúng.
a)
b)
Trong cả hai trường hợp a,b đều có 6 đoạn thẳng đó là
AB, BC, CD, DA, AC, BD
Đúng 0
Bình luận (0)