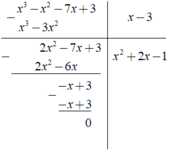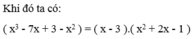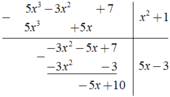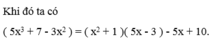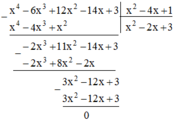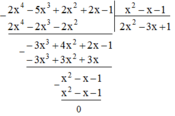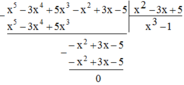Sắp xếp đa thức theo lũy thừa giảm dần của biến rồi làm phép chia: (x3 – 7x + 3 – x2) : (x – 3)

Những câu hỏi liên quan
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia: x 3 - 7 x + 3 - x 2 : ( x - 3 ) .
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia: 5 x 3 + 7 - 3 x 2 : ( x 2 + 1 )
Sắp xếp đa thức theo lũy thừa giảm dần của biến rồi làm phép chia: (2x4 – 3x3 – 3x2 – 2 + 6x) : (x2 – 2)
2x4 – 3x3 – 3x2 – 2 + 6x = 2x4 – 3x3 – 3x2 + 6x – 2
Thực hiện phép chia:
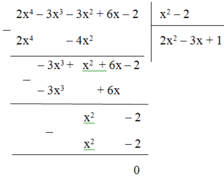
Vậy (2x4 – 3x3 – 3x2 + 6x – 2) : (x2 – 2) = 2x2 – 3x + 1.
Đúng 1
Bình luận (0)
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
12
x
2
-
14
x
+
3
-
6
x
3
+
x
4
:
1...
Đọc tiếp
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia: 12 x 2 - 14 x + 3 - 6 x 3 + x 4 : 1 - 4 x + x 2
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia :
a) \(\left(x^3-7x+3-x^2\right):\left(x-3\right)\)
b) \(\left(2x^4-3x^3-3x^2-2+6x\right):\left(x^2-2\right)\)
a) (x3 – 7x + 3 – x2) : (x – 3)

b) (2x4 – 3x2 – 3x2 – 2 + 6x) : (x2 – 2)

Xem thêm tại: http://loigiaihay.com/bai-67-trang-31-sgk-toan-8-tap-1-c43a4815.html#ixzz4ensEy1dY
Đúng 0
Bình luận (0)
Cho hai đa thức
f
(
x
)
-
2
x
2
-
3
x
3
-
5
x
+
5
x
3
-
x
+
x
2
+
4
x
+
3
+
4
x...
Đọc tiếp
Cho hai đa thức
f ( x ) = - 2 x 2 - 3 x 3 - 5 x + 5 x 3 - x + x 2 + 4 x + 3 + 4 x 2 , g ( x ) = 2 x 2 - x 3 + 3 x + 3 x 3 + x 2 - x - 9 x + 2
a. Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến
a. Ta có:
f(x) = -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2
= 2x3 + 3x2 - 2x + 3 (0.5 điểm)
g(x) = 2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2
= 2x3 + 3x2 - 7x + 2 (0.5 điểm)
Đúng 0
Bình luận (0)
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
2
x
2
-
5
x
3
+
2
x
+
2
x
4
-
1
:...
Đọc tiếp
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia: 2 x 2 - 5 x 3 + 2 x + 2 x 4 - 1 : x 2 - x - 1
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
x
5
-
x
2
-
3
x
4
+
3
x
+
5
x
3
-...
Đọc tiếp
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia: x 5 - x 2 - 3 x 4 + 3 x + 5 x 3 - 5 : 5 + x 2 - 3 x
cho 2 đa thức :
P(x)=2x3-2x+x2-x3+3x+2 và Q(x)=x3-x2-x+1
a)Thu gọn và sắp xếp các đa thức P(x) theo lũy thừa giảm dần của biến
b)Tìm đa thức H(x) biết H(x)+Q(x)=P(x)
`a,`
`P(x)=2x^3-2x+x^2-x^3+3x+2`
`= (2x^3-x^3)+x^2+(-2x+3x)+2`
`= x^3+x^2+x+2`
`b,`
`H(x)+Q(x)=P(x)`
`-> H(x)=P(x)-Q(x)`
`-> H(x)=(x^3+x^2+x+2)-(x^3-x^2-x+1)`
`H(x)=x^3+x^2+x+2-x^3+x^2+x-1`
`= (x^3-x^3)+(x^2+x^2)+(x+x)+(2-1)`
`= 2x^2+2x+1`
Vậy, `H(x)=2x^2+2x+1.`
Đúng 1
Bình luận (0)
a.
\(P\left(x\right)=x^3+x^2+x+2\)
\(Q\left(x\right)=x^3-x^2-x+1\)
b.
\(H\left(x\right)+Q\left(x\right)=P\left(x\right)\Rightarrow H\left(x\right)=P\left(x\right)-Q\left(x\right)\)
\(\Rightarrow H\left(x\right)=x^3+x^2+x+2-\left(x^3-x^2-x+1\right)\)
\(\Rightarrow H\left(x\right)=2x^2+2x+1\)
Đúng 0
Bình luận (0)